Log analysis: lithology
| Development Geology Reference Manual | |

| |
| Series | Methods in Exploration |
|---|---|
| Part | Wireline methods |
| Chapter | Difficult lithologies |
| Author | Khaled Hashmy, Mark Alberty |
| Link | Web page |
| Store | AAPG Store |
The term difficult lithologies, as addressed here, refers to a formation composed of two or more mineralogies. The presence of two or more minerals significantly increases the difficulty of determining both porosity and lithology from wireline logs. This article reviews some common techniques that can be used to solve for lithology and porosity. It also addresses some commonly encountered lithologies and their characteristics relative to log responses.
Identifying the occurrence of difficult lithologies[edit]
The occurrence of difficult lithologies can be identified from the following sources:
- Local knowledge of formations in the area
- Cuttings from the well
- Mudlogs of the well
- Conventional core analysis
- Sidewall percussion core analysis
- Sidewall rotary core analysis
- Analysis of log responses
The methods to determine the occurrence of difficult lithologies from the first six sources just listed are not covered in this article. (For information on these sources, see Mudlogging: drill cuttings analysis and Mudlogging: the mudlog; also see Core description.)
Identifying the occurrence of difficult lithologies from logs can be formidable. Two crossplot techniques are commonly used to identify the occurrence of mineralogies: (1) the M-N crossplot and (2) the MID crossplot.
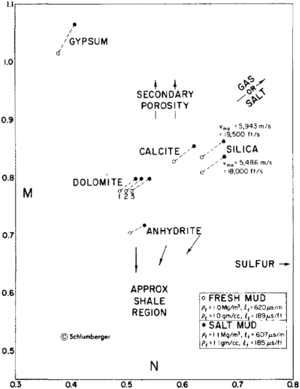
M-N crossplot[edit]
The M-N crossplot uses the density, compensated neutron, and compressional sonic logs to identify binary and ternary mixtures of minerals. The terms M and N are defined as follows:
These values are crossplotted in Figure 1. Binary mixtures of minerals plot along a line connecting the two mineral points. Ternary mixtures of minerals plot in a triangle connecting the three minerals points. Arrows indicate the effects of gas, salt, sulfur, secondary porosity, and shaliness.
MID crossplot[edit]
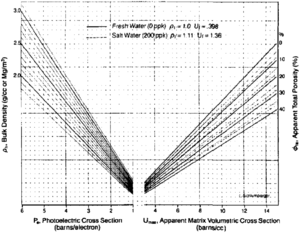
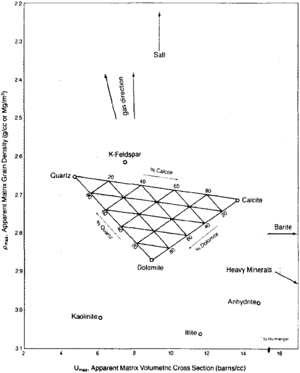
The MID or matrix identification crossplot uses the apparent volumetric cross section (UMAA) and the apparent matrix grain density (RHOMAA) to identify minerals. UMAA represents the projection of the volumetric photoelectric absorption index, U (the product of Pe and electronic density), to the value at zero porosity. RHOMAA results from a mathematical projection of the bulk density of an interval to its value at zero porosity. These projections to zero porosity effectively eliminate variance due to porosity, resulting in a variance mainly due to lithology.
This method requires that an estimate of total porosity be determined first. Typically, this can be done from a density-neutron crossplot (see Standard interpretation). Using this porosity, an apparent matrix density is determined from the following equation:
UMAA can be determined from the chart in Figure 2. Start by marking the Pe value on the photoelectric portion of the horizontal axis (left side), then go vertically to the bulk density value. Next, move horizontally to the apparent total porosity, and then down to the UMAA value.
Now you can cross plot the RHOMAA and UMAA values on the chart in Figure 3. Binary mixtures of minerals plot along a line connecting the two mineral points. Ternary mixtures of minerals plot in a triangle connecting the three mineral points. Arrows indicate the affects of gas, secondary porosity, salt, barite, and heavy minerals.
Techniques for analyzing difficult lithologies[edit]
Each logging measurement can be expressed in a response equation that relates the recorded log to the volumetric components of lithology and fluids. (For these response equations expressed in their most basic configuration, see Standard interpretation.) These basic equations can be expanded to include any number of mineralogies and fluids.
All the logging response equations can then be set up for each measurement, such as the density, neutron, and sonic. The unknowns must be less than or equal to the number of equations for a unique solution to be obtained. A paramount fact that must be kept in mind is that the number of variables that are being computed cannot exceed the number of equations. For example, if the density, neutron, and sonic logs are being used, the total number of equations that can be set up is four—one for each of the measured logs and the fourth for the material balance equation (exemplifying that the sum of all constituents equals 100% of the volume of the rock). Thus, in this case, only four variables can be computed. Assumptions and local knowledge can be used to constrain the problem by reducing the amount of unknown knowledge.
Once these logging relationships are established for the difficult lithology being addressed, a number of methods are available to solve these equations effectively for a solution. The more commonly used methods are
- Graphical crossplots
- Linear matrix solutions
- Weighted least squares minimization
Graphical crossplots[edit]
A wide variety of crossplots are used for analysis. Basically, these crossplots are designed for use with two porosity measurements and are all generally published in vendor chartbooks. The three most common crossplots are discussed here.
Density-compensated neutron crossplot[edit]
This type of crossplot is used for binary mixtures of sandstone and limestone, limestone and dolomite, dolomite and anhydrite, and sandstone and shale.
Sonic-compensated neutron crossplot[edit]
Two versions of the sonic-compensated neutron crossplot exist, one that uses the Wyllie time average equation and the other the Raymer-Hunt-Gardner equation for the sonic porosity relationship. These are used typically for binary mixtures of sandstone and limestone or limestone and dolomite. However, the sonic-compensated neutron crossplot is not particularly useful in fractured or vuggy formations.
Density-sonic crossplot[edit]
Two versions of the density-sonic crossplot also exist, one using the Wyllie time average equation and the other the Raymer-Hunt-Gardner equation for the sonic porosity relationship. These are used typically for binary mixtures of sandstone, limestone, or dolomite with gypsum, trona, salt, or sylvite. This plot is not particularly useful in fractured or vuggy formations nor for sandstone and limestone or limestone-dolomite mixtures.
Linear matrix solutions[edit]
Linear matrix solutions are almost always performed on a computer. A matrix is developed for each of the unknowns with the response equations used to describe the relationship between each element of the matrix. The computer uses a matrix solver to find the unique solution to the problem. The response equations must be linear for this system to work. This drawback leads to oversimplification of the response equations, which can result in degradation of the answers.
Weighted least squares minimizations[edit]
The weighted least squares minimization method is always performed on a computer. A number of commercial packages exist, including Global and Elan from Schlumberger, Optima from Western Atlas, ULTRA from Halliburton, and Probe from Scientific Software. Although these software packages are similar in general principle, they differ in individual methods of implementation, flexibility, and assignment of uncertainty.
This methodology uses an algorithm to search the range of possible answers to the problem to find the single answer that best fits the response equations and the measured logs. The equations are not required to be strictly linear, although as the response equation become somewhat nonlinear, the search becomes more difficult and time consuming. An incoherence function is output which is usually a useful indicator of the reliability of the answer (low incoherence is good). These programs are usually very flexible in the input of assumptions and allow virtually any type of mineralogy to be solved.
Types of difficult lithologies[edit]
The more commonly encountered difficult lithologies include
- Shaly sandstones
- Evaporites
- Carbonates
- Metamorphic and igneous rocks
- Volcanic and tuffaceous rocks
Shaly sandstones[edit]
The interpretation method best suited for shaly sandstones is dependent upon the distribution of shale, the clay type, the mineralogy of the silt fraction, and the resistivity of water within the sandstones. The classic approach is the sand-silt-shale method introduced by Poupon et al.[1] An approximate correction for a single heavy mineral was provided for in this approach. Silt is considered to be primarily quartz. Volume of clay, volume of silt, and porosity are determined from interpolation of the density-neutron crossplot. Matrix response points are defined for sand and silt, water, and dry clay minerals. A wet clay point is defined on the dry clay minerals-100% water line. A shale point was defined on the quartz-wet clay line. The model can then determine porosity, shale volume, and silt index from interpolation in this framework. Water saturation can be determined using an appropriate shaly sandstone resistivity equation. This method does not adequately address the more complex case of shaly sandstones with variable volumes of feldspar, mica, or carbonate material. This model can be solved using the graphical, linear matrix, or least squares minimization method.
The solution for the complex case of sandstones with feldspar, mica, and carbonate material was resolved after log analysts became comfortable with the new spectral gamma ray (K, Th, and U) and photoelectric (Pe) measurements. The spectral gamma ray log is helpful in sandstones containing potassium feldspars or thorium-bearing clays. The natural gamma ray spectra, Pe, density, and neutron expanded response equations can be combined to solve for porosity and to estimate volumes of calcite, quartz, dolomite, clay, feldspar, anhydrite, and salt. Once porosity is determined, saturation can be estimated from the appropriate shaly sandstone resistivity equation. This model is too complex to address using graphical methods and must be done using the linear matrix or least squares minimization method.
The distribution of shale and the salinity of formation water can significantly affect the resistivity of the formation. A variety of saturation models have been developed over the years to describe the influence of these factors. Some commonly used equations are as follows:
Simandoux:
Indonesia:
Dual water:
Waxman and Smits:
For a more complete explanation of water saturation equations and their terms, refer to Worthington[2] or Patchett and Herrick.[3] The Simandoux and Indonesia equations were designed mainly for relatively salty formation waters and moderate amounts of dispersed clay. The dual water and Waxman and Smits equations were designed for all water salinities and moderate amounts of dispersed clays.
Recommended logs to use for interpreting shaly sandstones are
Carbonates and evaporites[edit]
Carbonates and evaporites can complicate the interpretation process through the occurrence of fractures and vugs. The three primary porosity devices—the density, compensated neutron, and sonic—respond differently to the presence of fractures and vugs. The density investigates one side of the borehole, while the compensated neutron averages the formation properties around the borehole. The sonic generally does not respond to the secondary porosity associated with either fractures or vugs. This unequal response to these properties can lead to significant problems in determining lithology from any of the methods, as they generally presume that all the porosity devices see a common porosity and lithology.
Binary mixtures of carbonates or evaporites can be evaluated using graphical crossplot approaches. The density-neutron is generally the most used approach. This method will solve for sandstone-limestone, limestone-dolomite, or dolomite-anhydrite mixtures.
More complicated mixtures are best handled using the linear matrix or preferably the weighted least squares minimization technique. Additional minerals can be identified by incorporating the photoelectric, spectral gamma ray, and sonic logs. Some log measurements do not provide any relevant information in a given section. If the K, Th, and U values are uniformly low in the evaporite minerals, these logs have no resolving ability and are of little help in determining the rock constituents. If dolomite contains uranium, the uranium log is diagnostic.
Recommended logs to use for interpreting carbonates and evaporites are
- Dual laterolog or dual induction
- Density with photoelectric effect
- Compensated neutron
- Compensated sonic
- Spectral gamma ray
Metamorphic, igneous, and volcanic sequences[edit]
The approach to the interpretation of these sequences is similar to that of the carbonate sequences. Evaluation of tuffites and tuffaceous sandstones has been successful using compensated sonic, density, and compensated neutron crossplots on which the minerals form a Uthologic triangle of silica, light tuffite, and heavy tuffite. Models can easily be established for igneous and metamorphic sequences using the linear equations or the weighted least squares minimization approaches. The methods require the identification of the appropriate mineral matrix responses. Table 1 lists the log matrix responses of common minerals.
| Name | Formula | ρlog g/cc | φsnp p.u. | φcnl p.u. | Δtc μs/ft | Δts μs/ft | Pe barn/elect | U barn/cc | ε farads/m | tp nsec/m | GR APR units | Σ c.u. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SILICATES | ||||||||||||
| Quartz | SiO2 | 2.64 | 1. | 2. | 56.0 | 88.0 | 1.81 | 4.79 | 4.65 | 7.2 | — | 4.26 |
| β -Cristobalite | SiO2 | 2.15 | 2. | 3. | 1.81 | 3.89 | — | 3.52 | ||||
| Opal (3.5% H2 O) | SiO2 (H2 O)1209 | 2.13 | 4. | 2. | 58. | 1.75 | 3.72 | — | 5.03 | |||
| Garnet | Fe3 AI2 (SiO4 )3 | 4.31 | 3. | 7. | 11.09 | 47.80 | — | 44.91 | ||||
| Hornblende | Ca2 NaMg2 Fe2 AISi8 O22 (O,OH)2 | 3.20 | 4. | 8. | 43.8 | 81.5 | 5.99 | 19.17 | — | 18.12 | ||
| Tourmaline | NaMg3 AI6 B3 Si6 O2 (OH)4 | 3.02 | 16. | 22. | 2.14 | 6.46 | — | 7449.82 | ||||
| Zircon | ZrSiO4 | 4.50 | –1. | 3. | 69.10 | 311. | — | 692 | ||||
| CARBONATES | ||||||||||||
| Calcite | CaCO3 | 2.71 | 0 | –1. | 49.0 | 88.4 | 5.08 | 13.77 | 7.5 | 9.1 | — | 7.08 |
| Dolomite | CaCO3 MgCO3 | 2.85 | 2. | 1. | 44.0 | 72. | 3.14 | 9.00 | 6.8 | 8.7 | — | 4.70 |
| Ankerite | Ca(Mg,Fe)(CO3 )2 | 2.86 | 0 | 1. | 9.32 | 26.65 | — | 22.18 | ||||
| Siderite | FeCO3 | 3.89 | 5. | 12. | 47 | 14.69 | 57.14 | 6.8 – 7.5 | 88 91 | — | 52.31 | |
| OXIDATES | ||||||||||||
| Hematite | Fe2 O3 | 5.18 | 4. | 11. | 42.9 | 79.3 | 21.48 | 111.27 | — | 101.37 | ||
| Magnetite | Fe3 O4 | 5.08 | 3. | 9. | 73. | 22.24 | 112.98 | — | 103 08 | |||
| Geothite | FeO(OH) | 4.34 | 50 + | 60 + | 19.02 | 82.55 | — | 85 37 | ||||
| Limonite | FeO(OH)(H2 O)2 05 | 3.59 | 50 + | 60 + | 56.9 | 102.6 | 13.00 | 46.67 | 9.9–10.9 | 10.5–11.0 | — | 71.12 |
| Gibbsite | AI(OH)3 | 2.49 | 50 + | 60 + | 1.10 | — | 23.11 | |||||
| PHOSPHATES | ||||||||||||
| Hydroxyapatite | Ca5 (PO4 )3 OH | 3.17 | 5. | 8. | 42. | 5.81 | 18.4 | — | 9.60 | |||
| Chlorapatite | Ca5 (PO4 )3 CI | 3.18 | 1. | 1. | 42. | 606 | 19.27 | — | 130.21 | |||
| Fluorapatite | Ca5 (PO4 )3 F | 3.21 | 1. | 2. | 42. | 5.82 | 18.68 | — | 8.48 | |||
| Carbonapatite | (Ca5 (PO4 )3 )2 CO3 H2 O | 3.13 | 5. | 8. | 5.58 | 17.47 | — | 9.09 | ||||
| FELDSPARS-Alkali | ||||||||||||
| Orthoclase | KAISi3 O8 | 2.52 | 2. | 3. | 69. | 2.86 | 7.21 | 4.4–6.0 | 7.0–8.2 | ~220 | 15.51 | |
| Anorlhoclase | KAISi3 O8 | 2.59 | 2. | 2. | 286 | 7.41 | 4.4–6.0 | 7.0–8.2 | ~220 | 15.91 | ||
| Microciine | KAISi3 O8 | 2.53 | –2. | –3. | 2.86 | 7.24 | 4.4–6.0 | 7.0–8.2 | ~220 | 15.58 | ||
| FELDSPARS-Plagioclase | ||||||||||||
| Albite | NaAISi3 O8 | 2.59 | – 1. | –2. | 49. | 85. | 1.68 | 4.35 | 4.4–6.0 | 7.0–8.2 | — | 7.47 |
| Anorthite | CaAl2 Si2 O8 | 2.74 | –1. | 2. | 45. | 3.13 | 8.58 | 4.4–6.0 | 7.0–8.2 | — | 7.24 | |
| MICAS | ||||||||||||
| Muscovite | KAl2 (Si3 AIO10 )(OH)2 | 2.82 | 12. | 20. | 49. | 149. | 2.40 | 6.74 | 6.2–7.9 | 8.3–9.4 | ~270 | 16.85 |
| Glauconite | K2 (Mg,Fe)2 Al6 (Si4O10)3(OH)2 | ~2.54 | ~23. | ~38. | 6.37 | 16.24 | 24.79 | |||||
| Biotite | K(Mg,Fe)3 (AISi3 O10 (OH)2 | ~2.99 | ~11. | ~21. | 50.8 | 224. | 6.27 | 18.75 | 4.8–6.0 | 7.2–8.1 | ~275 | 29.83 |
| Phlogopite | KMg3 (AISi3 O10 (OH)2 | 50. | 207. | 33.3 | ||||||||
| CLAYS | ||||||||||||
| Kaolinite | AI4 Si4 O10 (OH)8 | 2.41 | 34. | 37. | 1.83 | 4.44 | ~5.8 | ~8.0 | 80–130 | 14.12 | ||
| Chlorite | (Mg,Fe,AI)6 (Si,AI)4 O10 (OH)8 | 2.76 | 37. | 52. | 6.30 | 17.38 | ~5.8 | ~8.0 | 180–250 | 24.87 | ||
| llite | K1.15 Al4 (Si76.5 AI11.5 )O20 (OH)4 | 2.52 | 20. | 30. | 3.45 | 8.73 | ~5.8 | ~8.0 | 250–300 | 17.58 | ||
| Montmorillonite | (Ca,Na),(AI,Mg,Fe)4 (Si, AI)8 O20 (OH)4 (H2 O)n | 2.12 | 40. | 44. | 2.04 | 4.04 | ~5.8 | ~8.0 | 150–200 | 14.12 | ||
| EVAPORITES | ||||||||||||
| Halite | NaCI | 2.04 | –2. | –3. | 67.0 | 120. | 4.65 | 9.45 | 5.6 – 6.3 | 7.9–8.4 | — | 754.2 |
| Anhydrite | CaSO4 | 2.98 | 1. | 2. | 50. | 5.05 | 14.93 | 6.3 | 8.4 | — | 12.45 | |
| Gypsum | CaSO4 (H2 O)2 | 2.35 | 50 + | 60 + | 52. | 3.99 | 9.37 | 4.1 | 6.8 | — | 18.5 | |
| Trona | Na2 CO4 NaHCO3 H2 O | 2.08 | 24. | 35. | 65. | 0.71 | 1.48 | — | 15.92 | |||
| Tachydrite | CaCl2 (MgCI2 )2 (H2 O)t2 | 1.66 | 50 + | 60 + | 92. | 3.84 | 6.37 | — | 406.02 | |||
| Sylvite | KCI | 1.86 | –2. | 3. | 8.51 | 15.83 | 4.6–4.8 | 7.2–7.3 | 500 + | 564.57 | ||
| Carnalite | KCIMgCI2 (H2 O)6 | 1.57 | 41. | 60 + | 4.09 | 6.42 | ~220 | 368.99 | ||||
| Langbenite | K2 SO4 (MgSO4 )2 | 2.82 | 1. | 2. | 3.56 | 10.04 | ~290 | 24.19 | ||||
| Polyhalite | K2 SO4 MgSO4 (CaS04 )2 (H2 O)2 | 2.79 | 14. | 25. | 4.32 | 12.05 | ~200 | 23.70 | ||||
| Kainite | MgSO4 KCI(H2 O)4 | 2.12 | 40. | 60 + | 3.50 | 7.42 | ~245 | 195.14 | ||||
| Kieserite | MgSO4 H2 O | 2.59 | 38 | 43. | 1.83 | 4.74 | — | 13.96 | ||||
| Epsomite | MgSO4 (H2 O)2 | 1.71 | 50 + | 60 + | 1.15 | 1.97 | — | 21.48 | ||||
| Bischofite | MgC12 (H2 O)6 | 1.54 | 50 + | 60 + | 100. | 2.59 | 3.99 | — | 323.44 | |||
| Barite | BaSO4 | 4.09 | –1. | 2. | 266 82 | 1091. | — | 6.77 | ||||
| Celestite | SrSO4 | 3.79 | –1. | –1. | 55.19 | 209. | — | 7.90 | ||||
| SULFIDES | ||||||||||||
| Pyrite | FeS2 | 4.99 | –2. | 3. | 39.2 | 62.1 | 16.97 | 84.68 | — | 9010 | ||
| Marcasite | FeS2 | 4.87 | –2 | 3. | 16.97 | 82.64 | — | 88.12 | ||||
| Pyrrhotite | Fe7 SB | 4.53 | 2. | –3. | 20.55 | 93.09 | — | 94.18 | ||||
| Sphalerite | ZnS | 3.85 | 3. | 3. | 35.93 | 138.33 | 7.8–8.1 | 9.3–9.5 | — | 25.34 | ||
| Chalopyrite | CuFeS2 | 4.07 | 2. | 3. | 26.72 | 108.75 | — | 102.13 | ||||
| Galena | PbS | 6.39 | 3. | 3. | 1631.37 | 10424. | — | 13.36 | ||||
| Sulfur | S | 2.02 | 2. | –3. | 122. | 5.43 | 10.97 | — | 20.22 | |||
| COALS | ||||||||||||
| Anthracite | CH358 N009 KO022 | 1.47 | 37. | 38. | 105. | 0.16 | 0.23 | — | 8.65 | |||
| Bituminous | CH793 N015 O078 | 1.24 | 50 + | 60 + | 120. | 0.17 | 0.21 | — | 14.30 | |||
| Lignite | CH849 N015 O211 | 1.19 | 47. | 52. | 160. | 0.20 | 0.24 | — | 12.79 | |||
Recommended logs to use for interpreting metamorphic and igneous sequences are
- Dual laterolog or dual induction
- Density with photoelectric effect
- Compensated neutron
- Compensated sonic
- Spectral gamma ray
See also[edit]
- Dipmeters
- Formation evaluation of naturally fractured reservoirs
- Basic open hole tools
- Basic tool table
- Determination of water resistivity
- Preprocessing of logging data
- Wireline formation testers
- Basic cased hole tools
- Standard interpretation
- Quick-look lithology from logs
- Borehole imaging devices
References[edit]
- ↑ Poupon, A., W. R. Hoyle, and A. W. Schmidt, A. W., 1971, Log analysis in formations with complex lithologies: Journal of Petroleum Technology.
- ↑ Worthington, P., 1985, The evolution of shaly-sand concepts in reservoir evaluation: The Log Analyst.
- ↑ Patchett, J. G., and D. C. Herrick, 1982, A review of saturation models: SPWLA Reprint Volume Shaly Sands, SPWLA.