Plate tectonics and basin formation

From AAPG Wiki
Jump to navigation Jump to search
Wiki Write-Off Entry
AAPG-WIKI-Write-off.jpg
Student Chapter University of Indonesia
Competition June 2015

Plate tectonics regards the lithosphere broken into plate that are in motion. The plates move relative to another along plate boundaries, sliding upon the underlying asthenosphere (the layer below the lithosphere that is formed of molten rock). The theory of plate tectonics emerged since the 1960s, and until now this theory has successfully explained various geological events, such as earthquakes, tsunamis, and volcanic eruption, also explained how the formation of mountains, continents, and oceans.

Plate Tectonics Map [1]

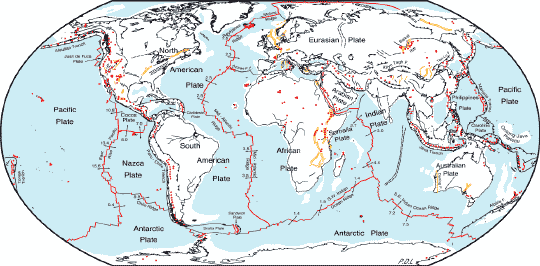
List of Tectonic Plates

The lithosphere is divided into several tectonic plates intersect with each other. Here are Earth's tectonic plates:

Major Plates (≥10 million km2)

These ten plates comprise the bulk of the continents and the Pacific Ocean.

  • Pacific Plate – 103,300,000 km2
  • North American Plate – 75,900,000 km2
  • Eurasian Plate – 67,800,000 km2
  • African Plate – 61,300,000 km2
  • Antarctic Plate – 60,900,000 km2
  • Australian Plate – 47,000,000 km2
  • South American Plate – 43,600,000 km2
  • Somali Plate – 16,700,000 km2
  • Nazca Plate – 15,600,000 km2
  • Indian Plate – 11,900,000 km2

Minor Plates (≥ 1 million km2, ≤ 10 million km2)

  • Philippine Sea Plate – 5,500,000 km2
  • Arabian Plate – 5,000,000 km2
  • Caribbean Plate – 3,300,000 km2
  • Cocos Plate – 2,900,000 km2
  • Caroline Plate – 1,700,000 km2
  • Scotia Plate – 1,600,000 km2
  • Burma Plate – 1,100,000 km2
  • New Hebrides Plate – 1,100,000 km2

Micro Plates (≤ 1 million km2)

African Plate

Antarctic Plate

  • Kerguelen microcontinent
  • Shetland Plate
  • South Sandwich Plate

Caribbean Plate

  • Panama Plate
  • Gonâve Microplate

Cocos Plate

  • Rivera Plate

Eurasian Plate

  • Adriatic or Apulian Plate
  • Aegean Sea Plate (or Hellenic Plate)
  • Amurian Plate
  • Anatolian Plate
  • Azores Microplate[5]
  • Banda Sea Plate
  • Iberian Plate
  • Iranian Plate
  • Molucca Sea Plate
  • Halmahera Plate
  • Sangihe Plate
  • Okinawa Plate
  • Pelso Plate
  • Sunda Plate
  • Timor Plate
  • Tisza Plate
  • Yangtze Plate

Australian Plate

  • Capricorn Plate
  • Futuna Plate
  • Indian Plate
  • Kermadec Plate
  • Maoke Plate
  • Niuafo'ou Plate
  • Sri Lanka Plate
  • Tonga Plate
  • Woodlark Plate

Juan de Fuca Plate

  • Explorer Plate
  • Gorda Plate

North American Plate

  • Greenland Plate
  • Okhotsk Plate

Pacific Plate

  • Balmoral Reef Plate
  • Bird's Head Plate
  • Caroline Plate
  • Conway Reef Plate
  • Easter Plate
  • Galapagos Plate
  • Juan Fernandez Plate
  • Kula Plate
  • Manus Plate
  • New Hebrides Plate
  • North Bismarck Plate
  • North Galapagos MicroPlate
  • Solomon Sea Plate
  • South Bismarck Plate

Philippine Sea Plate

  • Mariana Plate
  • Philippine Microplate

South American Plate

  • Altiplano Plate
  • Falklands Microplate
  • North Andes Plate

Plate Motion

The tectonic plates of the earth is not stationary, but moves relative with the speed of 1 to 10 cm per year. The movement of the earth's crustal plates that collide with each other will form the subduction zone and cause the forces acting both horizontally and vertically, which will form the folds of the mountains, volcanoes track or magmatic, fracturing the rock, and the lines of tectonic earthquakes and the formation of a particular region. Moreover, that will also form various types of deposition of sedimentary basins such as trench, fore arc basin, back arc basin, and basin between the mountains.

Plate Boundaries

Based on the direction of its movement, the plate boundary between tectonic plates with the other plate boundaries are divided into three types.

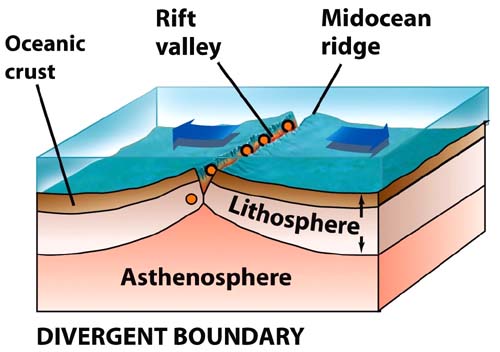
Divergent Plate Boundaries

Divergent plate boundaries occurs on two tectonic plates are break apart. When a broken plate tectonics, lithospheric thinning layer and split, forming divergent boundaries. In the ocean plate, this process causes the seafloor spreading. While on the continental shelf, this process causes the formation of rift valley due to the gap between the two plates which are away from each other.

Mid-Atlantic Ridge is one of the most famous examples of divergent, stretching from north to south along the Atlantic Ocean, restricting the Continent of Europe and Africa to the Americas.

Divergent Plate Boundary [2]

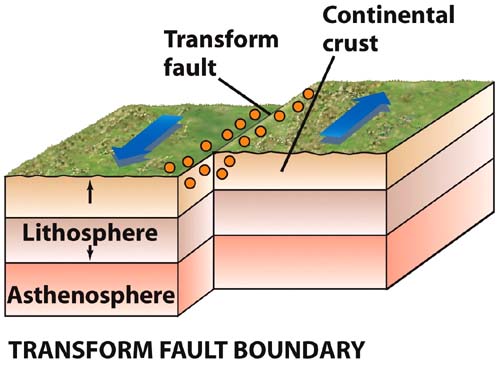
Transform Boundaries

At transform boundaries, one plate slides horizontally past another plate, the plate can occur on a single fault or on a group of parallel faults. Transform boundary is also known as transform fault. The most common type of transform fault occurs along fracture zones and connect two divergent plate boundaries at the crest of the mid-oceanic ridge.

The example of transform boundaries is the friction between the plates of the Pacific Ocean to the North American mainland plate which resulted the formation of the San Andreas Fault which extends along approximately 1,200 km from San Francisco in the north to the south of Los Angeles in the United States.

Transform Boundary [3]

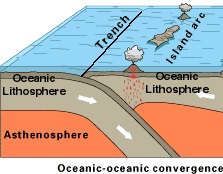
Convergent Plate Boundaries

Convergent plate boundaries are the collisions between tectonic plates. The collisions between tectonic plates can be distinguished into ocean-ocean convergent, ocean-continent convergent, or continent-continent convergent. The character of the boundary depends partly on the type of plates that converge. In ocean-ocean convergent, a plate can move toward another plate, where one plate subducts under the other. While, in ocean-continent convergent, the dense oceanic plate subducts under the continental plate. In continent-continent convergent, the two approaching plate collide and crumple but neither is subducted.[4]

Ocean-Ocean Convergent [5]
Ocean-Continent Convergent [6]
Continent-Continent Convergent [7]

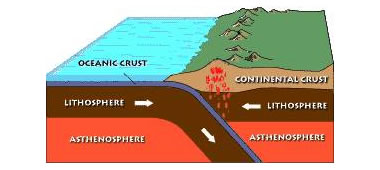
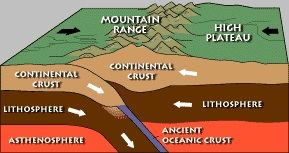
The Cause of Plate Motion

Mantle Convection

The widely accepted opinion regarding the cause of the plates move at this time is because of the convection currents in the mantle. The heat from the core of the Earth is transferred to the surface of the Earth through the mantle. The heat from the core warms up the liquid rock on mantle that closest to the core, causing the liquid rock to expand and rise toward the crust. The cooler liquid rock near the surface sinks back down toward the core. In doing so, a current of liquid rock is set up flowing toward the surface and back down again. This mantle convection is believed the causes the plates movement.

Mantle Convection [8]

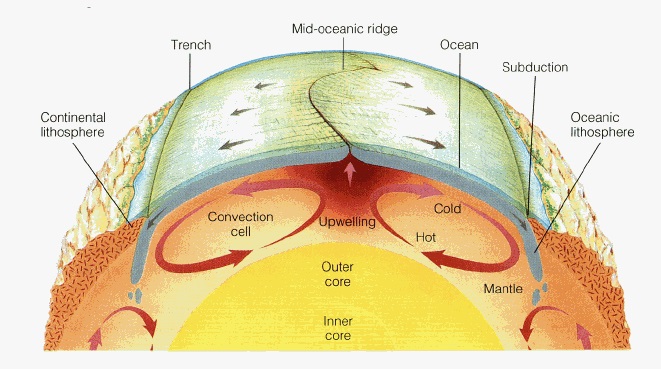
Ridge Push

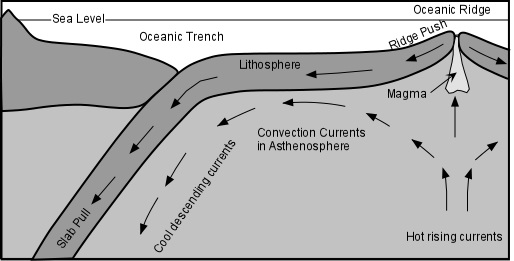
Ridge Push and Slab Pull Mechanism [9]

Ridge push or sliding plate force is a proposed mechanism for plate motion in plate tectonics. When a plate moves away from a divergent boundary, it cools and thickens. Cooling sea floor subsides as it moves, and this subsidence forms the broad side slopes of the mid-ocean ridge. An even more important slope form on the base of the lithosphere mantle. The mantle thickens as cooling converts asthenospheric mantle to lithospheric mantle. Therefore, the boundary between them is a slope down which the lithosphere slides. The oceanic plate is thought to slide down this slope at the base of lithosphere, which may have a relief of 80 to 1000 kilometres.[4]

Slab Pull

The other proposal is called slab pull. Cold lithosphere sinking at a steep angle through hot mantle should pull the surface part of the plate away from the ridge crest and then down into mantle as it cools. A subduction plate sinks because it is denser than the surrounding mantle. This density contrast is partly due to the fact that sinking lithosphere is cold. The subduction plate may also increase its density while it sinks, as low-density materials such as water are lost and as plate minerals collapse into denser form during subduction. Slab pull is thought to be at least twice as important as ridge push in moving an oceanic plate away from aridge crest. Slab pull causes rapid plate motion.[4]

Continental Drift

Continental Drift [10]

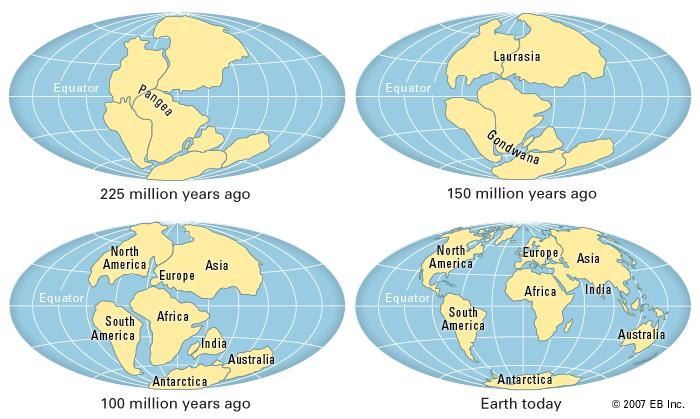
The revolution in the science of earth has been started since the early 19th century, when the emergence of a radical thought at that time to propose a hypothesis about the continents that move on the surface of the earth. Actually, the theory of plate tectonics already emerged when the idea of the Flotation hypothesis Continent (continental drift) was introduced first time by Alfred Wegener (1915) in his book "The Origins of Oceans and Continents". An effect of this floatation continent hypothesis is a hypothesis which assumes that the continents that exist today united formerly known as the super-continent called Pangaea. This super-continent Pangaea allegedly formed 200 million years ago which was then fragmented into pieces smaller then migrate or drifted into position as it is today.

Proof of the existence of the super-continent Pangaea 200 million years ago supported by the facts as follows:

The similarity of shorelines

The lack of compatibility coastline in the eastern part of the South American continent with a coastline of the western part of the African continent. Both this coastline when matched to one another will coincide. Wegener suspected that both continents were originally one. Based on the lack of compatibility shape of the coastline was then Wegener tried to match all the continents on earth.

The discovery of fossils from animals and plants are widespread and separated on several continents

  • Cynognathus fossil, a reptile that lived about 240 million years ago and was found in the South American continent and the African continent.
  • Mesosaurus fossil, a reptile that lived in freshwater lakes and rivers that lived about 260 million years ago, was found in the South American continent and the African continent.
  • Lystrosaurus fossil, a reptile that lived on land around 240 million years ago, was found in the continent of Africa, India and Antarctica.
  • Clossopteris fossils, a plant that lived 260 million years ago, was found in the continent of Africa, South America, India, Australia, and Antarctica.

The evidence of ancient climate

Earth scientist has also been studying the ancient climate, where in 250 million years ago was known that the southern hemisphere at the time it happened a cold climate, where the southern hemisphere was covered by a very thick layer of ice, such as in Antarctica, Australia, South America, Africa, and India. The areas that affected by glaciation in mainland Africa turned constantly to the equatorial region. However, this argument was later rejected, because for a period of glaciation in the southern hemisphere, the northern hemisphere tropical climates was characterized by the development of tropical swamp forests were extremely widespread and was the origin of the coal deposits in America eastern, Europe and Asia.

At this time, experts believe that the new terrestrial land experiencing glaciation came from the mainland, known as the super-continent Pangaea that located deep in the southern part of the current position. The evidence of Wegener to support the hypothesis of continental drift that newly acquired after 50 years of prior public geoscientists believe the truth of the hypothesis of continental drift.

The similarity of rock type

The Appalachian mountain path are located in the eastern part of the North American continent with the spread trending northeast and suddenly disappear on the beach Newfoundlands. Mountains that has a same age with the Appalachian mountains are also found in the British Isles and Scandinavia. Both of these mountains would form a continuous mountain paths. By way of uniting or matching the appearance of geological forms that separated by an ocean is needed, but the data are not sufficient to prove the hypothesis of a continental drift. In other words, if a continent has experienced separation from one another, it is absolutely necessary evidence that the geological structure and rock types is suitable or appropriate. Although the evidence of geological appearance is matched between the continents, but it is not enough to prove that the continent has undergone floatation.

Basin Formation

One of the geologic events can be explained by the theory of plate tectonics was the formation of basin.

What's Basin?

Basin in geology is defined as a low area in the Earth’s crust, of tectonic origin, in which sediments accumulate. Basins range in size from as small as hundreds of meters to large parts of ocean basins.

How basin can be created? On some cases with a small scale, fault movements can create relief of hundreds to thousands of meters laterally, resulting in small but often deep basins. But, the other main reason is because the continent rift. In plate tectonic theory, if one of plates rifting into pieces diverging apart then new basins being born, followed by motion reversal, convergence back together, plate collision, and mountain building.

The Wilson Cycle

Wilson cycle is a cycle opening and closing an ocean basin. Wilson cycle begins with a hypothetical geologically (tectonically) quiet continent. The model is divided into nine stages, but the stages are arbitrary and do not exist naturally. Within the earth is an ongoing series of processes and it is more important to understand these processes, how they are related, and how one process leads to the next process.

The Wilson Cycle [11]

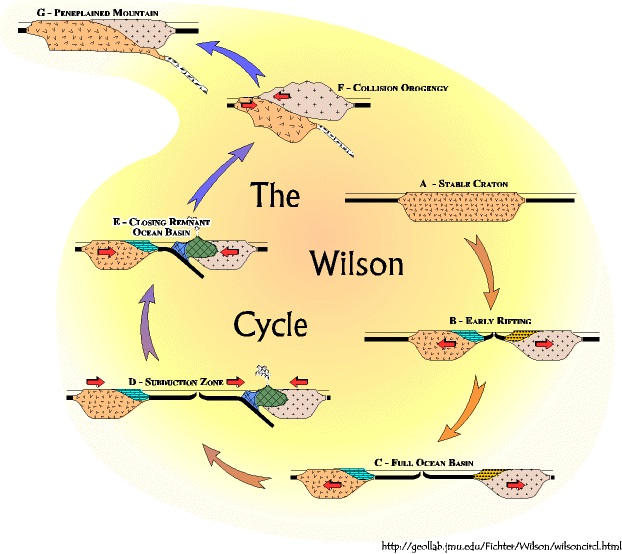
Stage A

The Wilson cycle begins in Stage A with a stable continental craton. A hot spot rises up under the craton, heating it, causing it to swell upward, stretch and thin like taffy, crack, and finally split into two pieces. This process not only splits a continent in two it also creates a new divergent plate boundary.

Stage B

The one continent has been separated into two continents, east and west, and a new ocean basin (the Ophiolite Suite) is generated between them. The ocean basin in this stage is comparable to the Red Sea today. As the ocean basin widens the stretched and thinned edges where the two continents used to be joined cool, become denser, and sink below sea level. Wedges of divergent continental margins sediments accumulate on both new continental edges.

Stage C

The ocean basin widens, sometimes to thousands of miles; this is comparable to the Atlantic ocean today. As long as the ocean basin is opening we are still in the opening phase of the Wilson cycle.

Stage D

The closing phase of the Wilson Cycle begins when a subduction zone (new convergent plate boundary) forms. The subduction zone may form anywhere in the ocean basin, and may face in any direction. In this model we take the simplest situation; a subduction zone developing under the edge of one continent. Once the subduction zone is active the ocean basin is doomed; it will all eventually subduct and disappear. These are remnant ocean basins.

Stage E

Most of the remnant ocean basin has subducted and the two continents are about to collide. Subduction under the edge of a continent has a lot of results. Deep in the subduction zone igneous magma is generated and rises to the surface to form volcanoes, that build into a cordilleran mountain range (e.g. the Cascade mountains of Washington, Oregon, and northern California.) Also, a lot of metamorphism occurs and folding and faulting.

Stage F

The two continents, separated in Stages A and B now collide. The remnant ocean basin is completely subducted. Technically the closing phase of the Wilson cycle is over. Because the subduction zone acts as a ramp the continent with the subduction zone (a hinterland) slides up over the edge of the continent without it (a foreland).

Stage G

Once the collision has occurred the only thing left for the mountain to do is erode down to sea level - a peneplain. The stage G drawing is a distortion, however. With the collision the continental thickness doubles, and since continental rock is light weight, both will rise as the mountain erodes, much like a boat rises when cargo is taken off of it. Thus, in reality, most of the hinterland continent will be eroded away, and the foreland continent will eventually get back to the earth's surface again. [12]

Basin Formation Method [13]

Basins form primarily in convergent, divergent and transform settings. Convergent boundaries create foreland basins through tectonic compression of oceanic and continental crust during lithospheric flexure. Tectonic extension at divergent boundaries where continental rifting is occurring can create a nascent ocean basin leading to either an ocean or the failure of the rift zone. In tectonic strike-slip settings, accommodation spaces occur as transpresional, transtensional or transrotational basins according to the motion of the plates along the fault zone and the local topography pull-apart basins.

Lithospheric Stretching

If the lithosphere is caused to stretch horizontally, by mechanisms such as ridge-push or trench-pull, the effect is believed to be two fold. The lower, hotter part of the lithosphere will flow slowly away from the main area being stretched, whilst the upper, cooler and more brittle crust will tend to fault and fracture. The combined effect of these two mechanisms is for the Earth's surface in the area of extension to subside, creating a geographical depression which is then often unfilled with water and/or sediments.

An example of a basin caused by lithospheric stretching is the North Sea - also an important location for significant hydrocarbon reserves. Another such feature is the Basin and Range province which covers most of the USA state of Nevada, forming a series of horst and graben structures.

Another expression of lithospheric stretching results in the formation of ocean basins with central ridges; The Red Sea is in fact an incipient ocean, in a plate tectonic context. The mouth of the Red Sea is also a tectonic triple junction where the Indian Ocean Ridge, Red Sea Rift and East African Rift meet. This is the only place on the planet where such a triple junction in oceanic crust is exposed sub-aerially. The reason for this is twofold, due to a high thermal buoyancy of the junction, and a local crumpled zone of seafloor crust acting as a dam against the Red Sea.

Lithospheric Compression or Shortening and Flexure

If a load is placed on the lithosphere, it will tend to flex in the manner of an elastic plate. The magnitude of the lithospheric flexure is a function of the imposed load and the flexural rigidity of the lithosphere, and the wavelength of flexure is a function of flexural rigidity alone. Flexural rigidity is in itself, a function of the lithospheric mineral composition, thermal regime, and effective elastic thickness. The nature of the load is varied. For instance, the Hawaiian Islands chain of volcanic edifices has sufficient mass to cause deflection in the lithosphere.

The obduction of one tectonic plate onto another also causes a load and often results in the creation of a foreland basin, such as the Po basin next to the Alps in Italy, the Molasse Basin next to the Alps in Germany, or the Ebro basin next to the Pyrenees in Spain.

Strike-Slip deformation

Deformation of the lithosphere in the plane of the earth occurs as a result of near horizontal maximum and minimum principal stresses. The resulting zones of subsidence are known as strike-slip or pull apart basins. Basins formed through strike-slip action occur where a vertical fault plane curves. When the curve in the fault plane moves apart, a region of transtension results, creating a basin. Another term for a transtensional basin is a rhombochasm. A classic rhombochasm is illustrated by the Dead Sea rift, where northward movement of the Arabian Plate relative to the Anatolian Plate has caused a rhombochasm.

The opposite effect is that of transpression, where converging movement of a curved fault plane causes collision of the opposing sides of the fault. An example is the San Bernardino Mountains north of Los Angeles, which result from convergence along a curve in the San Andreas Fault system. The Northridge earthquake was caused by vertical movement along local thrust and reverse faults bunching up against the bend in the otherwise strike-slip fault environment. In Nigeria, the dominant type of basement rock intersected by wells drilled for hydrocarbons, limestone, or water is granite. The three sedimentary basins in Nigeria are underlain by continental crust except in the Niger delta, where the basement rock is interpreted to be oceanic crust. Most of the wells that penetrated the basement are in the Eastern Dahomey embayment of western Nigeria. A maximum thickness of about 12,000 m of sedimentary rocks is attained in the offshore western Niger delta, but maximum thicknesses of sedimentary rocks are about 2000 m in the Chad basin and only 500 m in the Sokoto embayment.

References

  1. ↑ Nasa Earth Observatory
  2. ↑ http://science7soham.weebly.com/uploads/2/3/3/3/23339682/3633292_orig.jpg
  3. ↑ http://academic.brooklyn.cuny.edu/geology/grocha/plates/images/transform1.jpg
  4. ↑ 4.0 4.1 4.2 Carlson, Plummer, Hammersley. Physical Geology: Earth Revealed'. 9th edition. New York: The McGraw-Hill Companies, Inc, 2011. ISBN 978-0-07-122184-9
  5. ↑ http://oceansjsu.com/images/exp5_oceanocean_conv.gif
  6. ↑ http://geology.com/usgs/gold-prospecting/convergent-boundary-and-magma.jpg
  7. ↑ http://geomaps.wr.usgs.gov/parks/pltec/contvscont289x153.gif
  8. ↑ http://research.bpcrc.osu.edu/education/rr/plate_tectonics/mantle_convection_cell.gif
  9. ↑ http://www.tulane.edu/~sanelson/images/mantleconvect.gif
  10. ↑ http://media-1.web.britannica.com/eb-media/99/101699-004-066A8D00.jpg
  11. ↑ http://csmres.jmu.edu/geollab/Fichter/PlateTect/Images/wilsncircl.gif
  12. ↑ http://csmres.jmu.edu/geollab/vageol/vahist/wilsonsimp.html
  13. ↑ https://en.wikipedia.org/wiki/Sedimentary_basin

Other sources

Retrieved from "https://wiki.aapg.org/index.php?title=Plate_tectonics_and_basin_formation&oldid=26892"