Statistics overview

	Development Geology Reference Manual
Series	Methods in Exploration
Part	Geological methods
Chapter	Statistics overview
Author	T. C. Coburn, Brian R. Shaw
Link	Web page
Store	AAPG Store

The purpose of statistics is to project or infer, from limited samples, the character of a population. In most cases, particularly in oil and gas investigations, geological information is not derived from carefully designed sample schemes but, by design, represents anomalies. What successful company would drill on a regional trend as opposed to the top of a structure, on a bright spot, or at the crest of a reef? Statistical procedures presume that sufficient data are randomly sampled from a population and that the average sample value approximates the population average. This is only possible if both high and low values are sampled without bias and enough samples are taken to stabilize the calculations. While proper sampling techniques are essential to formal statistical inference, geological samples are much too difficult or costly to obtain and cannot be discarded. Therefore, the robust testing of hypotheses and calculation of confidence intervals for statistical projections must be viewed in the restrictive light of geological data. Nonetheless, quantitative description and relationship inferences can be made with the underlying awareness of the constraint of data quality.

It is also important to remember the effect of resolution and precision in analyzing quantitative geological data. J. C. Davis put it eloquently in his introduction to his classic text.^[1]

If you pursue the following topics, you will become involved with mathematical methods that have a certain aura of exactitude, that express relationships with apparent precision, and that are implemented on devices which have a popular reputation of infallibility.

While mathematical and statistical methods generate quantitative answers, one must always remain aware of the large disparity between geological samples and populations. Even in a producing field with “ample” well control, the creation of a structure map from well control represents the projection of a few 8-in. boreholes to hundreds of acres of surface area.

Even given this extreme difficulty, geological and statistical procedures share the common principle of parsimony: the simplest explanation is superior to a complex solution to a problem. Recognition of this relationship can form a basis for proper selection and application of the multitude of statistics available to the scientist.

Prior to beginning any statistical investigation, be sure to review any one of a number of overview texts in geological applications in the oil and gas industry, including Davis,^[1] Harbaugh et al.^[2] and Krumbein and Graybill.^[3]

Central tendency

Figure 1 An asymmetrical data set. The three measures of central tendency are different.

The simplest and most commonly overlooked statistical procedure is to plot the data.^[4] Often a simple crossplot reveals the essential characteristics of a data set and allows for interpretation as well as proper selection of additional methods. In most cases, plotting of data reveals the nature of the data set and outliers or anomalous data points to review for accuracy or measurement error and can indicate the spread or variability of the data. Eliminating measurement error is not uncommon even in commercial data sets. For example, in a data set composed of well information, if the kelly bushing is not known or uniformly subtracted from all wells, the resulting map will develop a severe case of volcanoes.

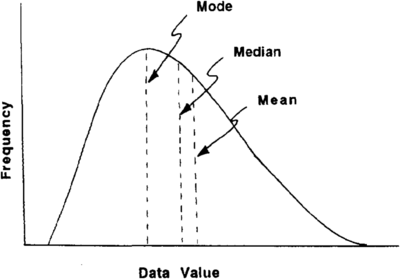
There are three measures of characterizing a population by describing the average value, or its central tendency. The most familiar measure is the arithmetic mean, which is simply the sum of the values divided by their number. The mode is the value that occurs with the greatest frequency, and the median is the value that has as many values above it as below it (Figure 1). As an example of comparing some of the statistics discussed in previous chapters, consider the following values of porosity (in percent) that have been measured on ten different sandstone samples: 15.1, 16.5, 18.8, 19.0, 22.0, 23.0, 25.0, 24.9, 31.9, and 43.0. Of the measures of central tendency, the arithmetic mean is the sum of all these numbers divided in this case by 10, or 239.2 ö 10 = 23.93. The median is 22.5 (halfway between 22.0 and 23.0), the value below which half the porosity values fall. The mid-range value is 29.05. The mode is the most frequently occurring value. Of the measures of dispersion, the range is computed to be 27.9, the variance is 61.79, and the standard deviation (the square root of the variance) is 7.86.

Although the mean, median, and mode convey the same general notion of centrality, their values are often different, as just demonstrated, because they represent different functions of the same data. Statistically, each has its strengths and weaknesses. Although it is sensitive to extreme values, the arithmetic mean is most generally used, partially because of convention and partially because of its computational versatility in other statistical calculations.

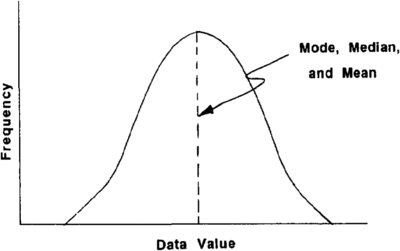
Figure 2 A symmetrical data set. The three measures of central tendency are identical.

The differences among these measures are a function of the frequency distribution of the samples. The frequency distribution is nothing more than a plot of the values versus the number of times the value occurs, and it is often depicted as a histogram. Most values cluster around some central value, and the frequency of occurrence declines toward extreme values. There are several shapes of frequency distributions that commonly occur in nature. Data sets that are symmetrical about a central value develop the familiar “bell-shaped” normal distribution (Figure 2). Data sets that have numerous small values and a few large values develop an asymmetrical curve shape. Comparison of histograms plays a vital role in the study of various geological properties. For example, construction of a histogram might be used to determine if a particular oil field exhibits a multimodal porosity distribution, indicating the presence of multiple lithologies. Another situation might involve a comparison of the distributions of petroleum field sizes discovered worldwide in foreland and rift basins.

The three measures of central tendency are identical in symmetrical data sets (Figure 2) and are very different in asymmetrical data sets (Figure 1). This difference is crucial in arriving at essential estimates. For example, what is the most likely value for reserves for the next well we drill? If, as in most producing basins, there are a few huge fields and many subcommercial small fields, the most likely discovery is not the mean but the mode. Determining the shape of the frequency distribution is critical to understanding which statistic to use. (For an excellent discussion of the characteristics of petroleum data population distributions, see Harbaugh et al.^[2])

Different geological properties and phenomena exhibit rather diverse distributions. For example, porosity is generally believed to be normally distributed, while permeability often tends to be lognormally distributed (that is, the logarithm of permeability tends to be normally distributed). Knowledge of the general form of the distribution is important to the selection of summary statistics because it helps prevent incorrect interpretations of the data. As a case in point, use of the arithmetic mean to represent average permeability is generally inappropriate because of the lognormality and high skewness of that property. Thus, the geometric mean, which identifies the median of a lognormal distribution, is better suited to this situation. In geology, not all quantities of interest approximate a normal distribution, and for that reason, uniform use of a particular statistic simply as a matter of convenience should be avoided. Table 1 lists formulas that are commonly used to derive effective permeability.

**Table 1** Commonly used formulas to derive effective permeability
Name	Formula	Application
Arithmetic mean	${\bar {k}}=\displaystyle {\frac {1}{H_{t}}}\displaystyle \sum \limits _{i=1}^{N}k_{i}h_{i}$	Average of uniform, horizontal, parallel layers in linear flow. k_j and h_j are the permeability and thickness of layer j . H_t is the total thickness.
Harmonic mean	${\bar {k}}=H_{t}\left(\displaystyle \sum \limits _{i=1}^{N}\displaystyle {\frac {h_{i}}{k_{i}}}\right)^{-1}$	Average of uniform, horizontal, serial layers in linear flow. Used for vertical permeability estimates in shale-free sands.
Geometric mean	${\bar {k}}=\left(\displaystyle \prod \limits _{i=1}^{N}k_{i}\right)^{1/N}$	Approximate average of an ensemble of uncorrelated random permeabilities in globally linear flow. k_j is the permeability of each element in the ensemble
Radial flow	${\bar {k}}=(k_{\rm {max}}\times k_{\rm {min}})^{1/2}$	Radial inflow (well) permeability in homogeneous, anisotropic media. k_max and k_min are the major and minor axes permeabilities.
Cross bedding	${\bar {k}}={\frac {\cos ^{2}\alpha }{k_{0}}}+{\frac {\sin ^{2}\alpha }{k_{90}}}$	Permeability in a direction at an angle a to cross bedding. k₀ and k₉₀ are the permeabilities parallel and perpendicular to cross bedding.

There are two basic types of measured data: discrete and continuous variables. Discrete variables are measurements that can only be represented by counted values. For example, the number of limestone beds in a formation or the number of producing wells in a field can only be whole numbers. Continuous variables can have any value within the scale of measurement. Gamma ray log values, the porosity or permeability of a rock, or the subsea elevation of a formation are examples of continuous variables. They can have fractional values and can even have values the same as a previous sample.

Variability

Another characteristic of a frequency distribution curve is that it indicates the spread or dispersion of values about the measure of central tendency. This is commonly called the variance and is referenced to the mean, which indicates an assumption of a normal distribution. The variance can be regarded as the average squared deviation of the sample population:

s^{2}={\frac {\displaystyle \sum (X-{\bar {x}})^{2}}{n}}

where

X = sample value
${\bar {x}}$ = sample mean
n = number of samples

The standard deviation is also used to describe the dispersion about the mean, and it is simply the square root of the variance. This statistic gives a measure of the variation in units of the variable instead of in squared units. For example, the variance of data measured in feet would be square feet or area. The standard deviation is the square root of this number, expressed in feet, which makes more sense for data measured in length.

Hypothesis testing

Inference in statistics is derived from sample data and projected to populations by comparing sample statistics to the underlying population frequency distribution derived statistic. Hypothesis testing thus involves the relationship of a sample statistic to the theoretical population value. The importance of determining the frequency distribution can easily be seen.

Statistical inference is generally presented as a true hypothesis to which a probability of not being true is assigned. The form of a statistical hypothesis is given both as the null or assumed event, H_o, and as the alternate event, H_a.

H_{\rm {o}}:\mu =\mu _{0}\quad H_{\rm {a}}:\mu \neq \mu _{0}

A confidence level, or probability of the decision being in error, must be specified to determine whether or not to accept the null hypothesis (in this case, the null hypothesis assumes that the sample mean is the same as the population mean, μ), or reject it in favor of the alternate hypothesis (which assumes that the means are different). Typical acceptable confidence level values for this decision have been derived from population frequency distribution equations and usually are 0.005, 0.01, 0.05, and 0.1.

Generally, the test for this type of hypothesis is the t-test. While there are many versions of hypotheses that can be tested using this statistic, the general form is that of comparing a hypothetical value obtained from two samples from the same population, with the value calculated given the sample variance:

t={\frac {{\bar {x}}_{1}-{\bar {x}}_{2}}{\sqrt {s_{{\bar {x}}_{1}}^{2}+s_{{\bar {x}}_{2}}^{2}}}}

where

{\bar {x}}_{1}

and

{\bar {x}}_{2}

= sample means

s_{{\bar {x}}_{1}}^{2}

and

s_{{\bar {x}}_{2}}^{2}

= sample variances

The hypothetical value can be obtained from generally available tables of t values, listed under the null hypothesis probability that was selected. If the t statistic exceeds the table value, then the null hypothesis, H_o, is rejected in favor of the alternate. Another way of phrasing this result is that the means are statistically different.

This type of hypothesis testing assumes that the variance of the population being tested is the same as the test statistic—in this case, a Student's t distribution—which is normally distributed and has a mean of 0 and a variance of 1. If the variable under consideration does not have a known population distribution of this character, it can be transformed to a standard normal distribution, which has a mean of 0 and a variance of 1. This is easily done by subtracting the mean from each observation and dividing by the sample standard deviation:

Z_{i}={\frac {X_{i}-{\bar {x}}}{s}}

where

Z_i = ith transformed variable
s = sample standard deviation

Confidence intervals around the population estimate also reflect the significance of a calculated statistic. A confidence interval is the range of possible values that contains the true value of the population estimate with some specified level of confidence or probability. For example, the confidence interval about the mean of a normal distribution can be represented by

{\bar {x}}-{\frac {t^{*}s}{\sqrt {n}}}\leq \mu \leq {\bar {x}}+{\frac {t^{*}s}{\sqrt {n}}}

where

t* = Student's f-distribution value
n = number of samples
s = sample standard deviation
μ = true population mean

The probability used for defining the t-distribution statistic also defines the range containing the true population value of the mean (μ).

References

↑ ^1.0 ^1.1 Davis, J. C., 1986, Statistics and data analysis in geology: New York, John Wiley, 646 p.
↑ ^2.0 ^2.1 Harbaugh, J. W., Doveton, J. H., Davis, J. C., 1977, Probability methods in oil exploration: New York, John Wiley, 269 p.
↑ Krumbein, W. C., Graybill, F. A., 1965, An introduction to statistical models in geology: New York, McGraw-Hill, 475 p.
↑ Atkinson, A. C., 1985, Plots, transformations, and regression: Oxford, U., K., Oxford Press, 282 p.

External links

find literature about
Statistics overview

[pt06r24-1] 1.0 ^1.1 Davis, J. C., 1986, Statistics and data analysis in geology: New York, John Wiley, 646 p.

[pt06r47-2] 2.0 ^2.1 Harbaugh, J. W., Doveton, J. H., Davis, J. C., 1977, Probability methods in oil exploration: New York, John Wiley, 269 p.

[pt06r68-3] Krumbein, W. C., Graybill, F. A., 1965, An introduction to statistical models in geology: New York, McGraw-Hill, 475 p.

[pt06r7-4] Atkinson, A. C., 1985, Plots, transformations, and regression: Oxford, U., K., Oxford Press, 282 p.

[1]

[2]

[3]

[4]

Statistics overview

Contents

Central tendency

Variability

Hypothesis testing

See also

References

External links

Navigation menu

Search