Uncertainties impacting reserves, revenue, and costs
| Development Geology Reference Manual | |

| |
| Series | Methods in Exploration |
|---|---|
| Part | Economics and risk assessment |
| Chapter | Uncertainties impacting reserves, revenue, and costs |
| Author | Peter R. Rose |
| Link | Web page |
| PDF file (requires access) | |
Each of the elements impacting the profit of an oil and gas property—reserves, production rates, costs and wellhead prices, and interest rates—is a prediction made under uncertainty. This fact alone means that "single-number estimates," which are deterministic projections, are usually inadequate for economic assessment of drilling ventures.
The problem is how to express our technical uncertainties realistically and in a form by which they can be utilized in economic equations and formulae. The most common convention in use today involves the formulation of a range of anticipated values for a given parameter, with probabilities—ordinarily 10%, 50%, and 90%—assigned to the values that comprise the range. For example, the geologist may think there is only a 10% chance that the anticipated pay zone will be less than 8 ft thick, 50% sure that it will be less than 12 ft thick, and 90% sure that it will be less than 18 ft thick. The same procedure can be applied to any parameter, including drainage area, production rate, decline rate, and wellhead prices.
However, such estimates cannot be "pulled out of the air"! They must rely on objective considerations of all relevant data, especially maps, cross sections, geophysical data, borehole log interpretations, analogous producing patterns, and other factors. Moreover, the geotechnical professional must arrive at a final distribution by "shaping it," that is, making trial estimates, examining the implications of various values in the distribution, comparing it with analog data, and adjusting it repeatedly until finally becoming comfortable with the estimates.
Biases in estimating[edit]
Unfortunately, a number of psychological biases exist, many of which are described by Tversky and Kahneman,[1] that tend to produce inconsistencies whenever we estimate under uncertainty (Table 1).
| Type of bias | Common example |
|---|---|
| Overconfidence | Estimators are much less accurate than they think they are. |
| Representativeness | Analog based on small sample size may not be truly analogous. |
| Availability | Recent or spectacular examples are more prone to be cited, regardless of their real frequency in nature. |
| Anchoring | In estimating, a low starting point leads to a lower final estimate, and a high starting point leads to a higher final estimate. |
| Unrecognized limits | Geologists forecasting future discoveries may disregard nongeological factors. |
| Motivation | Prospectors exaggerate the magnitude of reserves in order to sell the deal. |
| Conservatism | The feeling that overestimating a project is worse than underestimating it. |
For the development geologist, three such biases are especially dangerous:
- Overconfidence, which leads to excessively narrow ranges. People naturally tend to set predictive ranges that typically correspond to a confidence significantly lower than the ranges they think they are setting.[2]
- Conservatism, which leads to underestimates because professionals, fearing criticism, may feel it is worse to overestimate a project than to underestimate it.[3]
- Motivation, which leads to overestimates because of career or economic self-interest on the part of the professional in "selling the deal."[3]
The use of multiple independent estimators utilizing the same database, will go far toward reducing these various biases and producing accurate and consistent estimates. Also, systematic record keeping of geotechnical predictions versus outcomes and periodic review of such "before and after" data has proved to be helpful.
Lognormality and log probability paper[edit]
Most geological and production parameters are not distributed according to a symmetrical or normal distribution, that is, they do not form a bell-shaped frequency curve. Instead, they tend to produce a frequency distribution skewed to the right, so that there are many small values and only a few large ones. Such patterns approximate a lognormal distribution, and they arise from multiplication of several factors to produce one geological parameter.[4] [5] [6] Good examples include field sizes, production rates of wells in a field, porosity-feet (φh) of reservoirs, and effective well drainage area.
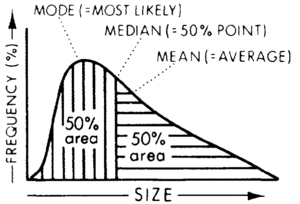
Here it is important to remind the reader that in a lognormal frequency distribution, the mode (or most likely point) is positioned to the left, at the peak of the curve. The median (or 50% point) lies in the middle, separating the area under the curve into two equal parts, whereas the mean (or average) lies to the right of the median (Figure 1). We shall be concerned mostly with the median and the mean in our estimates and calculations, generally discouraging use of the mode, as will be explained later.
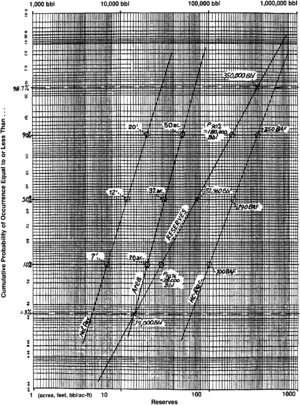
In combination with the cumulative probability curve, lognormality provides us with a very useful and powerful predictive tool. Accordingly, it is important to utilize (and understand) log probability paper. Although several forms are commercially available, the three-cycle type in which the probabilities extend from 0.01% to 99.99% is recommended (Figure 2).
Suppose you want to plot a distribution of field sizes from a basin or trend containing n number of fields.
- Prior to plotting the data, first arrange all n values in increasing order so that the final curve will be read as "cumulative probability of occurrence equal to or less than ..."
- To distribute all n values properly through the entire probability range, utilize the fractile approach in which the incremental spacing of values is determined by dividing n + 1 into 100. For example, in a distribution where n = 6, each value will be plotted at successive increments of 14.3%—14.3%, 28.6%, 42.9%, and so on.
- The procedure espoused here associates the 90% point
(P90%) with larger sizes and values, which are usually less likely. However, this is only a convention. Some workers switch P90% and P10% so that the high percentage (P90%) is associated with the lower value and the low percentage (P10%) goes with the higher value. Either procedure is acceptable, but you must be consistent.
- Any distribution that approximates lognormal will plot as an approximately straight line on log probability paper. The slope of the line is an expression of the variance. When the log probability paper is oriented so that the probability axis is vertical, as in this article, distributions expressing relative certainty (that is, small variance) have steep slopes, whereas those reflecting great uncertainty have more gentle slopes, often spanning three cycles or more on the log scale.
- When formulating a distribution, the geologist or engineer should work informally, shaping or sketching possible distributions on the log probability paper, moving back and forth among maps, sections, logs, and data sheets, and considering the implications of many probability levels. After many adjustments, the final curve or line will capture the perceived probability distributions.
- It is hard to overemphasize the power of independent multiple estimates. If it is possible to obtain and average three or four independent estimates derived from the same data set, the accuracy of the final estimate will nearly always be substantially improved.
- A useful way to begin is to select an absolute upper maximum possible value and plot it at the 99% position. Then select an absolute lower minimum possible value—some small but finite value—and plot it at the 1% position. Connect them with a straight line. Now, what value is associated with P50%? Is it reasonable? What about P90% and P10%? Are they reasonable high-side and low-side values? If not, move the line so that the P90% and P10% values are acceptable. Continue to adjust the curve until you are comfortable with all of its implications. The P99% and P1% plots are merely conventions to help you get started with the estimating process. It is expected that you will adjust these values as you work.
- Remember that the absolute maximum and minimum values are not P90% and P10%!
- Although the values associated with any conventional probabilities (P90%, P50%, and P10%) can be read directly from the log probability paper, neither the mode nor the mean is so apparent. These parameters must be calculated.
- The mean (or average) is the single best numerical representation of the distribution and is determined approximately by Swanson's Rule of approximation[7] as follows:
- Must all distributions be lognormal? A good working rule here is to assume lognormality, but be willing to modify or adjust the distribution if there is legitimate evidence (not just wishes or guesses) supporting it.
Combining distributions[edit]
Distributions can be combined using Monte Carlo or Latin hypercube simulation. These are routinely performed using available software and can involve almost any desired number of parameters.
However, a graphical shortcut is readily available for combining any three lognormally distributed factors. This procedure is quick and can be performed manually. The example shown in Table 2 uses area of drainage, average net pay, and hydrocarbon recovery factor. Other variables important in development evaluations include initial flow rate (IP), decline rate, wellhead prices, and costs.
| Area | Net Pay | HC Recovery | Reserves | Derived | ||
|---|---|---|---|---|---|---|
| P10% value | 20 ac | x 7 ft | x 100 bbl/ac-ft | = 14,000 bbl = P1.3% | P10% = 28,000 | Mza = 91,584 bbl |
| P50% value | 32 ac | x 12 ft | x 190 bbl/ac-ft | = 72,960 bbl = P50% | P50% = 72,960 | |
| P90% value | 50 ac | x 20 ft | x 350 bbl/ac-ft | = 350,000 bbl = P98.7% | P90% = 180,000 | |
| Meana (Mz) | 33.8 ac | x 12.9 ft | x x 211 bbl/ac-ft | = 92,000 bbl |
aApproximated by Swanson's rule
Note that multiplying the three P90% values for area, net pay, and hydrocarbon recovery does not yield a P90% value for reserves; in fact, it gives a product corresponding to 98.7%! Similarly, multiplying the three P10% values gives a reserves product that corresponds to P1.3%, not P10%.
However, we can put this to work. First, plot the P98.7% reserves product at P98.7% on the log probability paper and the P1.3% reserves product at P1.3%. Draw a line connecting them. The median value should lie on or near the line at P50%. Now, derive the values associated with P90% and P10% from the new reserves line and use them to solve for mean reserves using Swanson's Rule. Table 2 illustrates the calculations, and Figure 2 shows the graphical procedure. (As a reality check, you can also determine the mean values for area, net pay, and hydrogen recovery using Swanson's Rule, and then multiply them to yield a mean reserves figure that should approximate the previously calculated mean.)
This procedure works only when combining three distributions. But an analogous approach for combining two distributions utilizes the values of P92.7% and P7.3% (in place of P98.7% and P1.3%). This allows you to combine any reasonable number of variables into a final probability distribution by serial multiplications. Both approaches produce a mean that is accurate within about 3%—which is far more accurate than our precision in estimating such geotechnical parameters!
Field size and well size distributions[edit]
Within geologically consistent entities, such as basins, trends, or plays, populations of analogous oil and gas fields typically occur in lognormal distributions. This pattern becomes useful in several ways:
- Field size distributions (FSDs) drawn on log probability paper serve as useful reality checks (Megill, 1988)[7] against which prospects can be compared for purposes of perspective and likelihood.
- If realistic estimates can be made of minimum economic field size, FSDs can be used to determine the chance of commerciality, given that a discovery is indeed made. For example, if 20% of all fields in a producing trend are too small to return enough revenues to cover the costs to find, develop, and operate them (plus a reasonable profit on the investment), then we can expect one out of five new field discoveries in that trend to have found a noncommercial field.
- Commonly, wells within a field also show lognormal distribution, especially with regard to initial production rates and projected ultimate recoveries. Cumulative log probability plots of such parameters have great predictive value for the development geologist.
Accuracy levels in geotechnical predictions[edit]
Geologists, geophysicists, and engineers think they are much more accurate than they really are. In exploration forecasting, a goal of 0.5× to 2× for area of accumulation, net pay, and hydrocarbon recovery factor is about as accurate as nature will allow us to estimate. In other words, 80% of our predictions should be within an envelope of one-half to twice that of reality. Reserves predictions may vary more because of the multiplicity effect; perhaps 0.2× to 5× is a more reasonable range to expect here. Such variances can be portrayed on log probability paper.
Geologists working on development projects should do somewhat better than this, however, and perhaps a general range of 0.8× to 1.25× of actuality is expectable for predictions based on geological parameters and reservoir performance. Correspondingly, reserves predictions should fall within the 0.67× to 1.5× envelope for development wells, at the 80% confidence level.
Professionals interested in improving their performance in estimating will find that keeping records on predictions versus actuals will help them gradually improve their geotechnical forecasts.[3]
Other uncertainties in the economic equation[edit]
The remaining uncertainties involved in evaluating drilling ventures center around three main elements: reservoir performance, prices and costs, and taxes and regulatory costs.
Reservoir performance[edit]
An important uncertainty is reservoir performance, especially initial production rates, cumulative and ultimate production, and production decline rates. Field IPs and cumulative production tend to be lognormally distributed, whereas variations above or below typical decline rates seem to follow a more normal distribution.
Prices and costs[edit]
Prices and costs can be significant, especially wellhead prices, operating costs, inflation rates, and interest rates. Although many companies routinely project future increases in prices and costs in their economic analyses, the historical record indicates this practice may be misleading and unreliable. It is misleading because some marginal drilling ventures may become "commercial" only through such price escalation forecasts, and it is unreliable because the practice requires two forecasts to be made (price and cost escalation plus inflation rates), and the industry record at predicting either is demonstrably abysmal.
One procedure is to hold all wellhead prices and operating costs constant, assuming that they will rise or fall together. In addition, many firms now recognize that, by present standards, the historical price of oil has oscillated since 1880 between about $11 and $22 per barrel, (except for the 1978-1984 and 1990-1991 spikes), and they set their price predictions in that range. However, and costs are assumed and the inflation component of the discount rate is omitted (leaving a discount rate of approximately 3-4%), the project analyst is assuming that any price or cost changes that do occur will exactly offset any inflation or loss of purchasing power. If all the assumptions are correct, the result would be a constant purchasing power net present value.
Variations in oil prices would be expected to follow a lognormal statistical distribution, given a free world market—many small price fluctuations and only a few very large ones. However, predicting variations tends to be a near-term preoccupation, which is of limited value in a business that is as long-term as the oil business. Predicting trends would indeed be useful if we could do it—but the historical evidence says we cannot.
Predictive accuracy of cost forecasts for exploration ventures typically lies within the 0.5× to 2.0× range (80% of predictions are within one-half to twice the actual costs incurred). Because lower uncertainties ordinarily attend development projects, cost forecasts should be more accurate, perhaps within a range of about 0.80× to 1.25×.
Estimators who deliberately overestimate such costs to prevent cost overruns actually impose unnecessary burdens on project economics by making projects appear to be more expensive to carry out than they actually are. This may cause the firm to rule out many prospects and thereby suffer the opportunity loss that each rejected prospect represents. Ideally, such predictions should be objective so that cost overruns and underruns balance at the end of each drilling year.
Taxes and regulatory costs[edit]
Taxes and regulatory costs, which show substantial variation, can also be expressed as ranges. Commonly, however, the effect of such governmental regulatory activity is to delay project performance, thus reducing profitability because of the time value of money. There is a clear tendency for operators to underestimate both the number and duration of such delays.[2] It is also possible that future investments and operating costs will increase as a result of future regulatory activity.
See also[edit]
- Introduction to economics and risk assessment
- Risk: expected value and chance of success
- Economics: time value of money
- Risk: dealing with risk aversion
- Economics: fundamental equations for oil and gas property evaluation
- Economics: key parameters
- Economics of property acquisitions
- Cash flow model
References[edit]
- ↑ Tversky, A., and D. Kahneman, 1981, The framing of decisions and the psychology of choice: Science, v. 211, p. 453-458.
- ↑ 2.0 2.1 Capen, E. C., 1976, The difficulty of assessing uncertainty: Journal of Petroleum Technology, v. 28, p. 843-850.
- ↑ 3.0 3.1 3.2 Rose, P. R., 1987, Dealing with risk and uncertainty in exploration--how can we improve?: AAPG Bulletin, v. 71, n. 1, p. 1-16.
- ↑ Kaufman, G., 1963, Statistical decision and related techniques in oil and gas exploration: Englewood Cliffs, NJ, Prentice-Hall, 307 p.
- ↑ Capen, E. C., 1984, Why lognormal? in E. C.Capen, R. E. Megill, and P. R. Rose, ed., Prospect Evaluation: AAPG Course Notes: Tulsa, OK, AAPG, 8 p.
- ↑ Megill, R. E., 1984, An introduction to risk analysis, 2nd ed.: Tulsa, OK, PennWell Books, 274 p.
- ↑ 7.0 7.1 Megill, R. E., 1988, An introduction to exploration economics, 3rd ed.: Tulsa, OK, PennWell Books, 238 p.