Waterflooding

Development Geology Reference Manual
Series	Methods in Exploration
Part	Reservoir engineering methods
Chapter	Waterflooding
Author	A. M. Sam Sarem
Link	Web page
Store	AAPG Store

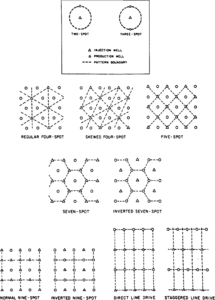
Waterflooding is a process used to inject water into an oil-bearing reservoir for pressure maintenance as well as for displacing and producing incremental oil after (or sometimes before) the economic production limit has been reached. This is done through the displacement of oil and free gas by water. In waterflooding, water is injected into one or more injection wells while the oil is produced from surrounding producing wells spaced according to the desired patterns. There are many different waterflood patterns used in the industry, the most common of which are illustrated in Figure 1.

Quick estimation of waterflood recovery

• 

  Figure 1 Flooding patterns.

• 

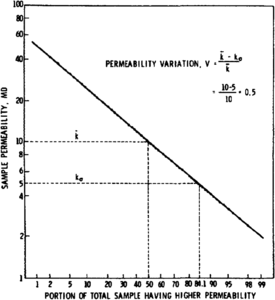
  Figure 2 Permeability variation example problem.

• 

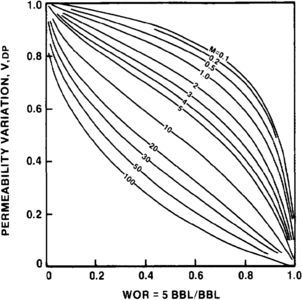
  Figure 3 Vertical sweep efficiency (coverage) as a function of WOR, M, and permeability variation (V_DP), where WOR = 5.

• 

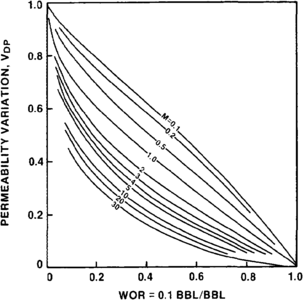
  Figure 4 Vertical sweep efficiency (coverage) as a function of WOR, M, and permeability variation (V_DP), where WOR = 0.1.

• 

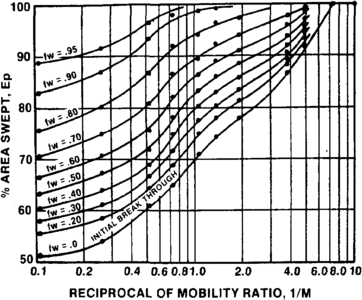
  Figure 5 Effect of mobility ratio on oil production for the five-spot pattern.

• 

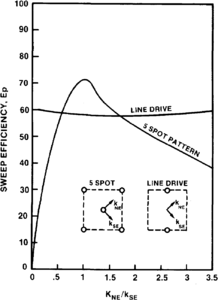
  Figure 6 Effect of directional permeability on sweep efficiencies for varied degrees of permeability anisotropes at a fluid mobility ratio of 1.

The overall recovery (E_R) is a product of displacement efficiency (E_D), invasion or vertical sweep efficiency (E_V) and the pattern or areal sweep efficiency (E_P).

$E_{\rm {R}}=E_{\rm {D}}\times E_{\rm {V}}\times E_{\rm {P}}$

where

• E_R = overall recovery (fraction of initial oil in place recovered)
• E_D = displacement efficiency or volume of oil displaced divided by total oil volume (fraction)
• E_V = vertical or invasion efficiency (fraction of vertical reservoir section contacted by injection fluid)
• E_P = pattern efficiency or pattern swept by total pattern area

The displacement efficiency is a function of residual oil saturation (S_or) of the swept region. The following equation gives the displacement efficiency as a function of S_or and the interstitial (irreducible) water saturation (S_wi):

$E_{\rm {D}}=(1-S_{\rm {or}}-S_{\rm {wi}})/(1-S_{\rm {wi}})$

where

• S_or = saturation of residual oil (fraction)
• S_wi = saturation of irreducible water (fraction)

The displacement efficiency depends upon the ratio of the viscous to capillary forces or capillary number. In enhanced recovery processes, the interfacial tension between the oil and water is reduced to improve the capillary number.

The vertical sweep efficiency is a function of the vertical heterogeneity (layering) and the mobility ratio (M). The mobility ratio defined here is the ratio of the relative permeability to water at S_or (k_rw) to the relative permeability of the oil at S_wi multiplied by the oil-water viscosity ratio (μ_o/μ_w) as expressed in the following equation:

$M=(k_{\rm {rw}}/k_{\rm {ro}})\times (\mu _{\rm {o}}/\mu _{\rm {w}})$

where

• M = mobility ratio, or the ratio of relative permeability to water at S_or divided by the relative permeability of oil at S_wi multiplied by the oil-water viscosity ratio
• k_rw = relative permeability of water
• k_ro = relative permeability of oil
• μ_o = viscosity of oil
• μ_w = viscosity of water

The vertical heterogeneity is most commonly described by the Dykstra-Parsons permeability variation (V_DP), defined as the ratio of the standard deviation of the permeability of various layers (σ) divided by the mean permeability ($({\bar {k}})$), as given in the following equation:

${\displaystyle V_{\rm {$DP}}=\sigma /{\bar {k}}}

where

• V_DP = Dykstra-Parsons permeability variation
• k = absolute permeability
• ${\bar {k}}$ = mean permeability or sum of the permeabilities divided by the number of permeabilities

In practice, the permeability variation is determined by arranging the permeabilities in descending order and determining the percent-greater-than values for each permeability. From a plot of k versus percent greater than on a log probability graph sheet (as shown in Figure 2), the values of k at 50% and k at 84.1% are read, and V_DP is determined as follows:

${\displaystyle V_{\rm {$DP}}=(k_{50}-k_{84.1})/k_{50}}

Dykstra and Parsons have published charts for determining the vertical sweep efficiency (V_D) or conformance from the mobility ratio and the permeability variation, as shown for WOR = 5 and 0.1 in Figures 3 and 4, respectively.

The pattern efficiency is a function of the previously defined mobility ratio, the flood pattern, and given water cut. Figure 5 shows the pattern efficiency as a function of mobility ratio and water cut for a five-spot pattern. Craig shows similar plots for several other common patterns.

A word of caution is appropriate at this point. The knowledge of directional permeability can be crucial in placement of pattern injectors. The injectors should always line up in the direction of maximum permeability. As shown in Figure 6, infill drilling can rotate the flow pattern and in some cases it can reduce the areal sweep efficiency, as exemplified in this figure for a five-spot and line-drive case. As shown, the sensitivity of the sweep efficiency to the ratio of maximum to minimum areal permeability depends heavily upon whether the maximum permeability is in the direction of injection to injection wells or injection to production wells.

Example of Estimation of Waterflooding Recovery:

Estimate the overall recovery of a five-spot waterflood for the following cases:

Case	VDP	M	WOR
1	0.7	3	0.1
2	0.7	1.5	0.1
3	0.5	1.5	0.1
4	0.7	3	5
5	0.5	3	5

Other properties are as follows:

• k_rw at S_or = 0.2
• k_ro at S_wi = 0.95
• μ_o = 10 cp at reservoir temperature
• μ_w = 0.7 cp at reservoir temperature
• S_or = 0.30
• S_wi = 0.28

Solution:

$E_{\rm {R}}=E_{\rm {D}}\times E_{\rm {V}}\times E_{\rm {P}}$

$E_{\rm {D}}=(1-S_{\rm {wi}}-S_{\rm {or}})/(1-S_{\rm {wi}})=(1-0.28-0.3)/(1-0.28)=0.583$

$M=(k_{\rm {rw}}/k_{\rm {ro}})\times (\mu _{\rm {o}}/\mu _{\rm {w}})=(10)(0.2)/(0.7)(0.95)=3.0$

The rest of the solution is given in the following table:

Case	VDP	M	WOR	ED	EV	EP	ER
1	0.7	3	0.1	0.583	0.06	0.57	0.02
2	0.7	1.5	0.1	0.583	0.09	0.61	0.03
3	0.5	1.5	0.1	0.583	0.27	0.61	0.10
4	0.7	3	5	0.583	0.5	0.835	0.24
5	0.5	3	5	0.583	0.185	0.57	0.06

Mathematical modeling of waterfloods

The foregoing analysis is one of many simplified approaches that can be taken as a first approximation for the prediction of waterflood recovery, as fully explained by Craig and Bradley. For a more accurate recovery prediction, mathematical modeling of the reservoir is essential. However, the most important aspect of reservoir modeling is the construction of the model, which requires detailed knowledge of the reservoir characteristics. Once the most probable reservoir realization is determined, the history matching of primary production can be used to refine the model before it is used to predict the waterflood behavior. For this purpose, any of the many commercially available softwares can be used.

See also

• Enhanced oil recovery
• Drive mechanisms and recovery
• Reservoir modeling for simulation purposes
• Reserves estimation
• Fluid flow fundamentals
• Introduction to reservoir engineering methods
• Petroleum reservoir fluid properties

External links

find literature about Waterflooding

• Original content in Datapages
• Find the book in the AAPG Store

drill pipe