Difference between revisions of "Amplitude variations with offset (AVO)"
Cwhitehurst (talk | contribs) |
|||
| (16 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | AVO has been a prominent technique in detecting hydrocarbons and reducing drilling risk. AVO can detect hydrocarbons because AVO shows the variation of the amplitude of the offset, which represents the amplitude of the wave energy as it passes through the layer which is influenced by the parameters of the speed and density of the coating, so that the density of the layer can be analyzed by analyzing the reflection coefficient. AVO means that amplitude change with offset caused by lithology of fluid. AVO is also known as AVA (amplitude variation with angle) because this phenomenon is based on the relationship between the reflection coefficient and the angle of incidence. But since the angle of incidence affecting the offset and the offset itself can be varied in order to change the angle of incidence ( | + | {{Wiki Write Off Entry |
| + | |image=AAPG-WIKI-Write-off.jpg | ||
| + | |student chapter=University of Indonesia | ||
| + | |competition=June 2015 | ||
| + | }} | ||
| + | AVO has been a prominent technique in detecting hydrocarbons and reducing drilling risk. AVO can detect hydrocarbons because AVO shows the variation of the amplitude of the [[offset]], which represents the amplitude of the wave energy as it passes through the layer which is influenced by the parameters of the speed and density of the coating, so that the density of the layer can be analyzed by analyzing the reflection coefficient. AVO means that amplitude change with offset caused by lithology of fluid. AVO is also known as AVA (amplitude variation with angle) because this phenomenon is based on the relationship between the reflection coefficient and the angle of incidence. But since the angle of incidence affecting the offset and the offset itself can be varied in order to change the angle of incidence ([[:File:Fig.1.incident angle.png|Figure 1]]), so it is commonly known as AVO. | ||
| − | [[File:Fig.1.incident angle.png|framed| | + | [[File:Fig.1.incident angle.png|center|framed|{{figure number|1|}}The incident angle is directly proportional to the offset <ref>www.wikiwand.com</ref>]] |
| − | Variation of reflection coefficient is the primary thing in analyzing AVO. It starts when the P-Waves hit the interface, if it is normal incidence ( | + | Variation of reflection coefficient is the primary thing in analyzing AVO. It starts when the P-Waves hit the interface, if it is normal incidence ([[:File:Fig.2.normal incidence.jpg|Figure 2]]), the coefficient reflections will be the difference of acoustic impedance (product of density and P velocity) over the sum. |
| + | |||
| + | <math>R_{NI}= \frac{\rho_2 \cdot Vp_2 - \rho_1\cdot Vp_1}{\rho_2 \cdot Vp_2 + \rho_1\cdot Vp_1} </math> | ||
Where RNI is the reflection coefficient. | Where RNI is the reflection coefficient. | ||
| − | [[File:Fig.2.normal incidence.jpg|framed|center| | + | [[File:Fig.2.normal incidence.jpg|framed|center|{{figure number|2|}}Normal Incidence<ref>www.ukm.my</ref>]] |
| − | While in the non-normal incidence (fig.3), some of the P-Waves that come will transform into the S waves so that there will be a reflection coefficient variation as a result of different Vp and Vs value. For example, when wave penetrates into a gas layer, the Vp will be decreasing and the Vs will be constant. It means that in certain condition there will be an anomaly in Vp/Vs. This anomaly will cause variation in the reflection coefficient whereas the coefficient itself is the main focus in AVO analysis | + | While in the non-normal incidence (fig.3), some of the P-Waves that come will transform into the S waves so that there will be a reflection coefficient variation as a result of different Vp and Vs value. For example, when wave penetrates into a gas layer, the Vp will be decreasing and the Vs will be constant. It means that in certain condition there will be an anomaly in Vp/Vs. This anomaly will cause variation in the reflection coefficient whereas the coefficient itself is the main focus in AVO analysis <ref>Choliq, M. T., 2007, Pemodelan parameter elastic batuan degan inversi AVO untuk karakterisasi reservoir hidrokarbon karbonat formasi baturaja: Jawa Barat Utara.</ref>. |
| − | [[File:Fig.3.Non-normal incidence.png|framed|center| | + | [[File:Fig.3.Non-normal incidence.png|framed|center|{{figure number|3|}}Non-normal incidence <ref> Stephen,Scott.(2011). University of Indonesia </ref>]] |
The relationship between the reflection coefficient and the angle of incidence in write down the Zoeppritz equations by Karl Zoeppritz since the early 20th century and then this equations was developed again by some figures such as Bortfeld (1961), Aki, Richard and Frasier (1976), Hilterman (1983), and Shuey (1985). | The relationship between the reflection coefficient and the angle of incidence in write down the Zoeppritz equations by Karl Zoeppritz since the early 20th century and then this equations was developed again by some figures such as Bortfeld (1961), Aki, Richard and Frasier (1976), Hilterman (1983), and Shuey (1985). | ||
| − | == Zoeppritz Equations == | + | ==Zoeppritz Equations== |
Zoeppritz derived the amplitudes of the reflected and transmitted waves using the conservation of stress and displacement across the layer boundary. | Zoeppritz derived the amplitudes of the reflected and transmitted waves using the conservation of stress and displacement across the layer boundary. | ||
| + | |||
| + | <math> \begin{bmatrix} | ||
| + | R_p\\ | ||
| + | R_s\\ | ||
| + | T_p\\ | ||
| + | T_r | ||
| + | |||
| + | \end{bmatrix} = \begin{bmatrix} | ||
| + | -\sin \Theta_1 & -\cos \Phi _1 & \sin\Theta _2 &\sin \Phi _2 \\ | ||
| + | \cos \Theta _1 &-\sin \Phi _1 &\cos \Theta _2 &-\sin \Phi _2 \\ | ||
| + | \sin 2\Theta _1 &\frac{Vp_1}{Vs_1}\cos 2\Phi _1 &\frac{\rho_2V_{s2}^{2}Vp_1}{\rho _1Vs_1^{2}Vp_2}\cos2\Phi _2 &\frac{\rho_2V_{s2}Vp_1}{\rho _1Vs_1^{2}}\cos2\Phi _2 \\ | ||
| + | -\cos 2\Phi _1 &\frac{Vs_1}{Vp_1}\sin 2\Phi _1 &\frac{\rho_2Vp_2}{\rho _1Vp_1}\cos2\Phi _2 &-\frac{\rho_2Vs_2}{\rho _1Vp_1}\sin 2\Phi _2 | ||
| + | \end{bmatrix}^{-1}\begin{bmatrix} | ||
| + | \sin \Theta _1\\ | ||
| + | \cos \Theta _1\\ | ||
| + | \sin 2\Theta _1\\ | ||
| + | \cos 2\Phi _1 | ||
| + | |||
| + | \end{bmatrix} </math> | ||
Because Zoeppritz equations give four equations with four unknowns, there are some of approximations in order to perform physical interpretation and visualization of the effect of some parameters to reflection coefficient. Some of the approximations are: | Because Zoeppritz equations give four equations with four unknowns, there are some of approximations in order to perform physical interpretation and visualization of the effect of some parameters to reflection coefficient. Some of the approximations are: | ||
| − | + | ===Bortfeld Approximation (1961)=== | |
With assumptions that there is slight change in the layer properties, Bortfeld generates this approximation : | With assumptions that there is slight change in the layer properties, Bortfeld generates this approximation : | ||
| − | + | <math> R(\Theta _1) = \frac{1}{2}\ln \left ( \frac{V_{p2}\rho _2\cos \theta _1}{V_{p1}\rho _1\cos \theta _2} \right )+\frac{\sin^{2}\theta_1}{V_{p1}}\left ( V_{s1}^{2}-V_{s2}^{2} \right )\left [ 2+\frac{\ln\left ( \frac{\rho _2}{\rho_1} \right )}{\ln\left ( \frac{Vp_2}{Vp_1} \right )- \ln\left ( \frac{Vp_2 Vs_1}{Vp_1Vs_2} \right )} \right ] </math> | |
| + | |||
| + | ===Aki, Richard and Frasier Approximation (1976)=== | ||
Bortfeld approximation then revised by Richard-Frasier (1976) and by Richard-Aki (1980). Approximation of Richard-Frasier is giving a simple equation because it is written in a clear three forms, namely the right-hand side includes the first P wave velocity, the second node density and the last wave velocity. | Bortfeld approximation then revised by Richard-Frasier (1976) and by Richard-Aki (1980). Approximation of Richard-Frasier is giving a simple equation because it is written in a clear three forms, namely the right-hand side includes the first P wave velocity, the second node density and the last wave velocity. | ||
| − | + | <math> R(\theta)= a\frac{\Delta Vp}{Vp}+ b \frac{\Delta \rho}{\rho}+ c \frac{\Delta Vs}{Vs} </math> | |
| + | |||
| + | where <math> a = \frac{1}{2\cos^{2}\theta}, b = 0.5-\left [ 2\left ( \frac{Vs}{Vp} \right )^{2}\sin^{2}\theta \right ], c = -4\left ( \frac{Vs}{Vp} \right )^{2}\sin^{2}\theta </math> | ||
| + | |||
| + | and | ||
| + | :<math> \rho = \frac{\rho_2+\rho_1}{2}, \Delta \rho = \rho_2 - \rho_1 </math> | ||
| + | :<math> Vp = \frac{Vp_2+Vp_1}{2}, \Delta Vp = Vp_2 - Vp_1 </math> | ||
| + | :<math> Vs = \frac{Vs_2+Vs_1}{2}, \Delta Vs = Vs_2 - Vs_1 </math> | ||
| + | :<math> \theta = \frac{\theta_2+\theta_1}{2} </math> | ||
| + | |||
| + | ===Hilterman (1983)=== | ||
Hilterman simplified Bortfeld equations by separating the reflection coefficients into the form of acoustic and elastic : | Hilterman simplified Bortfeld equations by separating the reflection coefficients into the form of acoustic and elastic : | ||
| − | + | <math> R(\theta_1) = \frac{Vp_2\rho_2\cos\theta_1 - Vp_1\rho_1\cos\theta_2}{Vp_2\rho_2\cos\theta_1 + Vp_1\rho_1\cos\theta_2 }+ \left ( \frac{\sin\theta_1 }{Vp_1}\right )\left ( Vs_1+Vs2 \right )\left [ 3\left ( Vs_1-Vs2 \right ) + \frac{2\left ( Vs_2\rho_1 - Vs_1\rho_2 \right )}{\rho_2 + \rho_1} \right ] </math> | |
| + | |||
| + | ===Shuey Approximation (1985)=== | ||
Shuey modified Aki and Richard equation by using variable of poisson ratio as follows: | Shuey modified Aki and Richard equation by using variable of poisson ratio as follows: | ||
| + | <math> R(\theta_1) = R_p + \left [ R_p A_o + \frac {\Delta\sigma}{1-\sigma^{2}} \right ]\sin^{2}\theta + \frac{\Delta\alpha }{2\alpha}\left ( \tan^{2}\theta-\sin^{2}\theta \right ) </math> | ||
| + | |||
| + | where | ||
| + | :<math> \sigma =\frac{\left ( \sigma _1+\sigma _2 \right )}{2}, \Delta \sigma = \left ( \sigma _2-\sigma _1 \right )</math> | ||
| + | :<math> A_o = B-2\left ( 1+B \right )\frac{1-2\sigma }{1-\sigma } </math> | ||
| + | :<math> B = \frac{\frac{\Delta \alpha }{\alpha }}{\frac{\Delta \alpha }{\alpha }+ \frac{\Delta \rho }{\rho }}</math> | ||
| − | == AVO Classification == | + | ==AVO Classification== |
| − | In 1989 Rutherford and Williams introduced a three-fold classification of AVO (amplitude versus offset) characteristics for seismic reflections from the interface between shales and underlying gas sands. The classification scheme they proposed is explicitly defined for gas sands and has become the industry standard; it has proven its validity and usefulness in countless exploration efforts. In 1997 Castagna and Swan proposed AVO crossplotting wherein an estimate of the normal-incidence reflectivity is plotted against a measure of the offset dependent reflectivity. Using this approach Castagna and Swan graphically illustrated the continuum between the classes and defined the characteristics of the classes using what they termed AVO Intercept and AVO Gradient. They also added a class 4 | + | In 1989 Rutherford and Williams introduced a three-[[fold]] classification of AVO (amplitude versus offset) characteristics for seismic reflections from the interface between shales and underlying gas sands. The classification scheme they proposed is explicitly defined for gas sands and has become the industry standard; it has proven its validity and usefulness in countless exploration efforts. In 1997 Castagna and Swan proposed AVO crossplotting wherein an estimate of the normal-incidence reflectivity is plotted against a measure of the [[offset]] dependent reflectivity. Using this approach Castagna and Swan graphically illustrated the continuum between the classes and defined the characteristics of the classes using what they termed AVO Intercept and AVO Gradient. They also added a class 4 <ref> Young, Roger A. and LoPiccolo, Robert D. (2004). Conforming and Non-conforming Sands – An Organizing Framework for Seismic Rock Properties. </ref>. |
| − | [[File:Fig.4.classification avo.jpg|framed|center|Fig.4. Classifications of AVO | + | [[File:Fig.4.classification avo.jpg|framed|center|Fig.4. Classifications of AVO <ref>Ahmed,Haseb. Institute of Geologi,University of the punjab </ref>]] |
| − | + | ===Class 1 : High impedance Gas-Sandstone=== | |
Class 1 sandstone has higher impedance than its cover (shale). Interface between shale and this kind of sandstone will generate a high reflection coefficient and a positive zero offset, but has amplitude magnitude decreasing in order to offset. Class 1 has greater gradient than class 2 and class 3. Sandstone at class 1 is having a change in polarity in certain angle, then the amplitude will be increasing proportionally to the offset. | Class 1 sandstone has higher impedance than its cover (shale). Interface between shale and this kind of sandstone will generate a high reflection coefficient and a positive zero offset, but has amplitude magnitude decreasing in order to offset. Class 1 has greater gradient than class 2 and class 3. Sandstone at class 1 is having a change in polarity in certain angle, then the amplitude will be increasing proportionally to the offset. | ||
| − | + | ===Class 2 : Near zero impedance contrast gas sandstone=== | |
Class 2 sandstone has almost equally acoustic impedance with its cover (seal rock) and the amplitude which is increasing proportionally to the offset. Class 2 sandstone divided into class 2 and class 2p. class 2 sandstone has negative reflection coefficient at zero offset while class 2p has positive at zero offset. | Class 2 sandstone has almost equally acoustic impedance with its cover (seal rock) and the amplitude which is increasing proportionally to the offset. Class 2 sandstone divided into class 2 and class 2p. class 2 sandstone has negative reflection coefficient at zero offset while class 2p has positive at zero offset. | ||
| − | + | ===Class 3 : Low impedance gas sandstone=== | |
Class 3 has lower acoustic impedance than its cover. | Class 3 has lower acoustic impedance than its cover. | ||
| − | + | ===Class 4=== | |
| − | Class 4 has negative reflection coefficient at zero offset and amplitude that is decreasing against the offset. There is a change in polarity at a certain angle and then amplitude will increasing proportionally to the offset. | + | Class 4 has negative reflection coefficient at zero offset and lower impedance with amplitude that is decreasing against the offset. There is a change in polarity at a certain angle and then amplitude will increasing proportionally to the offset. |
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |+Table 1. Behavior of the Various Gas Sand Classes | ||
| + | |- | ||
| + | ! Class || Relative Impedance || Amplitude Vs. Offset | ||
| + | |- | ||
| + | | I || Higher than overlying unit || Decreases | ||
| + | |- | ||
| + | | II || About the same as the overlying unit || Increase or decrease; may change sign | ||
| + | |- | ||
| + | | III || Lower than overlying unit || Increases | ||
| + | |- | ||
| + | | IV || Lower than overlying unit || Decreases | ||
| + | |} | ||
| + | |||
| + | ==References== | ||
| + | <references /> | ||
| + | *Rutherford,S.R. and Williams R.H. (1989). Amplitude-versus-offset Variations in Gas Sands. | ||
| + | *C. Ecker, D. Lumley, S. Levin, T. Rekdal, A. Berlioux, R. Clapp, Y. Wang & J. Ji. (2001). An AVO Analysis Project. | ||
| + | *http://www.ipt.ntnu.no/pyrex/stash/avo_theory.pdf , accessed on June 2015. | ||
Latest revision as of 21:39, 27 March 2019
| Wiki Write-Off Entry | |
|---|---|

| |
| Student Chapter | University of Indonesia |
| Competition | June 2015 |
AVO has been a prominent technique in detecting hydrocarbons and reducing drilling risk. AVO can detect hydrocarbons because AVO shows the variation of the amplitude of the offset, which represents the amplitude of the wave energy as it passes through the layer which is influenced by the parameters of the speed and density of the coating, so that the density of the layer can be analyzed by analyzing the reflection coefficient. AVO means that amplitude change with offset caused by lithology of fluid. AVO is also known as AVA (amplitude variation with angle) because this phenomenon is based on the relationship between the reflection coefficient and the angle of incidence. But since the angle of incidence affecting the offset and the offset itself can be varied in order to change the angle of incidence (Figure 1), so it is commonly known as AVO.
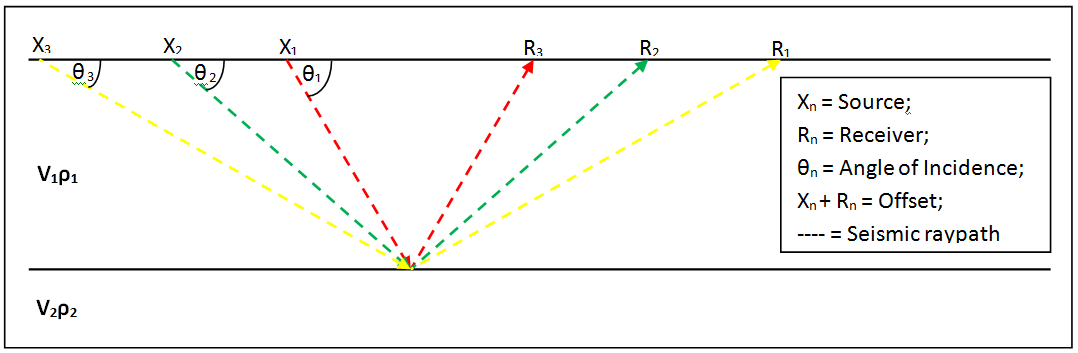
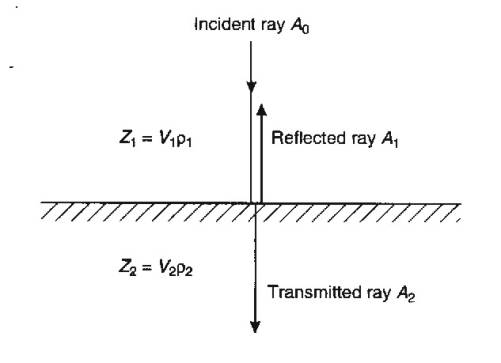
Variation of reflection coefficient is the primary thing in analyzing AVO. It starts when the P-Waves hit the interface, if it is normal incidence (Figure 2), the coefficient reflections will be the difference of acoustic impedance (product of density and P velocity) over the sum.
Where RNI is the reflection coefficient.
While in the non-normal incidence (fig.3), some of the P-Waves that come will transform into the S waves so that there will be a reflection coefficient variation as a result of different Vp and Vs value. For example, when wave penetrates into a gas layer, the Vp will be decreasing and the Vs will be constant. It means that in certain condition there will be an anomaly in Vp/Vs. This anomaly will cause variation in the reflection coefficient whereas the coefficient itself is the main focus in AVO analysis [3].
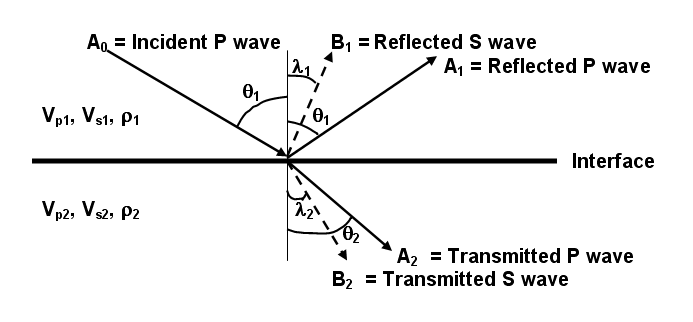
The relationship between the reflection coefficient and the angle of incidence in write down the Zoeppritz equations by Karl Zoeppritz since the early 20th century and then this equations was developed again by some figures such as Bortfeld (1961), Aki, Richard and Frasier (1976), Hilterman (1983), and Shuey (1985).
Zoeppritz Equations
Zoeppritz derived the amplitudes of the reflected and transmitted waves using the conservation of stress and displacement across the layer boundary.
Because Zoeppritz equations give four equations with four unknowns, there are some of approximations in order to perform physical interpretation and visualization of the effect of some parameters to reflection coefficient. Some of the approximations are:
Bortfeld Approximation (1961)
With assumptions that there is slight change in the layer properties, Bortfeld generates this approximation :
Aki, Richard and Frasier Approximation (1976)
Bortfeld approximation then revised by Richard-Frasier (1976) and by Richard-Aki (1980). Approximation of Richard-Frasier is giving a simple equation because it is written in a clear three forms, namely the right-hand side includes the first P wave velocity, the second node density and the last wave velocity.
where
and
Hilterman (1983)
Hilterman simplified Bortfeld equations by separating the reflection coefficients into the form of acoustic and elastic :
Shuey Approximation (1985)
Shuey modified Aki and Richard equation by using variable of poisson ratio as follows:
where
AVO Classification
In 1989 Rutherford and Williams introduced a three-fold classification of AVO (amplitude versus offset) characteristics for seismic reflections from the interface between shales and underlying gas sands. The classification scheme they proposed is explicitly defined for gas sands and has become the industry standard; it has proven its validity and usefulness in countless exploration efforts. In 1997 Castagna and Swan proposed AVO crossplotting wherein an estimate of the normal-incidence reflectivity is plotted against a measure of the offset dependent reflectivity. Using this approach Castagna and Swan graphically illustrated the continuum between the classes and defined the characteristics of the classes using what they termed AVO Intercept and AVO Gradient. They also added a class 4 [5].
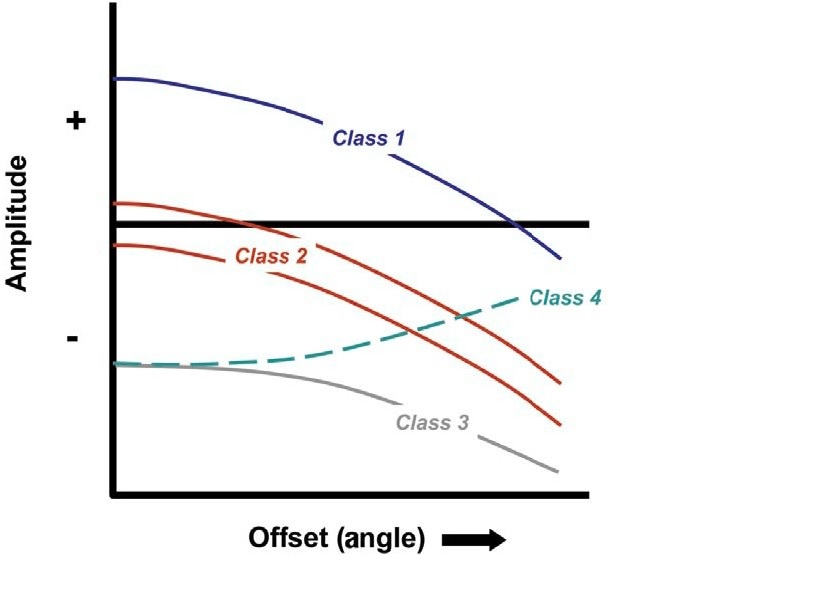
Class 1 : High impedance Gas-Sandstone
Class 1 sandstone has higher impedance than its cover (shale). Interface between shale and this kind of sandstone will generate a high reflection coefficient and a positive zero offset, but has amplitude magnitude decreasing in order to offset. Class 1 has greater gradient than class 2 and class 3. Sandstone at class 1 is having a change in polarity in certain angle, then the amplitude will be increasing proportionally to the offset.
Class 2 : Near zero impedance contrast gas sandstone
Class 2 sandstone has almost equally acoustic impedance with its cover (seal rock) and the amplitude which is increasing proportionally to the offset. Class 2 sandstone divided into class 2 and class 2p. class 2 sandstone has negative reflection coefficient at zero offset while class 2p has positive at zero offset.
Class 3 : Low impedance gas sandstone
Class 3 has lower acoustic impedance than its cover.
Class 4
Class 4 has negative reflection coefficient at zero offset and lower impedance with amplitude that is decreasing against the offset. There is a change in polarity at a certain angle and then amplitude will increasing proportionally to the offset.
| Class | Relative Impedance | Amplitude Vs. Offset |
|---|---|---|
| I | Higher than overlying unit | Decreases |
| II | About the same as the overlying unit | Increase or decrease; may change sign |
| III | Lower than overlying unit | Increases |
| IV | Lower than overlying unit | Decreases |
References
- ↑ www.wikiwand.com
- ↑ www.ukm.my
- ↑ Choliq, M. T., 2007, Pemodelan parameter elastic batuan degan inversi AVO untuk karakterisasi reservoir hidrokarbon karbonat formasi baturaja: Jawa Barat Utara.
- ↑ Stephen,Scott.(2011). University of Indonesia
- ↑ Young, Roger A. and LoPiccolo, Robert D. (2004). Conforming and Non-conforming Sands – An Organizing Framework for Seismic Rock Properties.
- ↑ Ahmed,Haseb. Institute of Geologi,University of the punjab
- Rutherford,S.R. and Williams R.H. (1989). Amplitude-versus-offset Variations in Gas Sands.
- C. Ecker, D. Lumley, S. Levin, T. Rekdal, A. Berlioux, R. Clapp, Y. Wang & J. Ji. (2001). An AVO Analysis Project.
- http://www.ipt.ntnu.no/pyrex/stash/avo_theory.pdf , accessed on June 2015.


![{\displaystyle R(\Theta _{1})={\frac {1}{2}}\ln \left({\frac {V_{p2}\rho _{2}\cos \theta _{1}}{V_{p1}\rho _{1}\cos \theta _{2}}}\right)+{\frac {\sin ^{2}\theta _{1}}{V_{p1}}}\left(V_{s1}^{2}-V_{s2}^{2}\right)\left[2+{\frac {\ln \left({\frac {\rho _{2}}{\rho _{1}}}\right)}{\ln \left({\frac {Vp_{2}}{Vp_{1}}}\right)-\ln \left({\frac {Vp_{2}Vs_{1}}{Vp_{1}Vs_{2}}}\right)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8730314821b541d3c506ca08d6d4a493635b00e9)

![{\displaystyle a={\frac {1}{2\cos ^{2}\theta }},b=0.5-\left[2\left({\frac {Vs}{Vp}}\right)^{2}\sin ^{2}\theta \right],c=-4\left({\frac {Vs}{Vp}}\right)^{2}\sin ^{2}\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ba088e0bcbaa4c0ebfe1ccef062d2098d83a3a0)




![{\displaystyle R(\theta _{1})={\frac {Vp_{2}\rho _{2}\cos \theta _{1}-Vp_{1}\rho _{1}\cos \theta _{2}}{Vp_{2}\rho _{2}\cos \theta _{1}+Vp_{1}\rho _{1}\cos \theta _{2}}}+\left({\frac {\sin \theta _{1}}{Vp_{1}}}\right)\left(Vs_{1}+Vs2\right)\left[3\left(Vs_{1}-Vs2\right)+{\frac {2\left(Vs_{2}\rho _{1}-Vs_{1}\rho _{2}\right)}{\rho _{2}+\rho _{1}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cba9ea4330ccbe7343ca59226676666fd3b3cdd0)
![{\displaystyle R(\theta _{1})=R_{p}+\left[R_{p}A_{o}+{\frac {\Delta \sigma }{1-\sigma ^{2}}}\right]\sin ^{2}\theta +{\frac {\Delta \alpha }{2\alpha }}\left(\tan ^{2}\theta -\sin ^{2}\theta \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea55f8277a08c4f79dea0a2fa9a9c59438de5df4)


