Hydrodynamics
| Exploring for Oil and Gas Traps | |

| |
| Series | Treatise in Petroleum Geology |
|---|---|
| Part | Critical elements of the petroleum system |
| Chapter | Formation fluid pressure and its application |
| Author | Edward A. Beaumont, Forrest Fiedler |
| Link | Web page |
| Store | AAPG Store |
Hydrodynamics describes lateral fluid movement through aquifers that have generally low dip. The fluids can have a vertical component to their movement but, on a basinwide scale, the lateral flow component is of major concern.
Hydraulic head
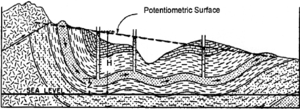
Hydraulic head (Hw) is the height or elevation above a given subsurface point at which a column connected to a body of water will equilibrate. It reflects the level of the potential energy possessed by the water.[2]
The equation for hydraulic head is
where:
- Hw = height above P (ft or m)
- Z = height (elevation) of P above a datum (ft or m)
- P = measured pressure (lb/ft2 or kg/cm2)
- ρ = density of fluid (lb/ft3 or g/cm3)
- g = coefficient of gravity (lb force/lb mass or kg force/kg mass)
Figure 1 illustrates the relationship of the variables Hw and Z used in the above equation.
Potential energy of fluids
Potential energy (Φ) is the driving force of fluid movement. Its magnitude depends on the hydraulic head (Hw) with respect to sea level and is expressed as
According to Dahlberg[2], hydraulic head serves as a practical approximation of fluid potential, since the only difference is the coefficient of gravity (g), which is fairly constant.
Potentiometric surface
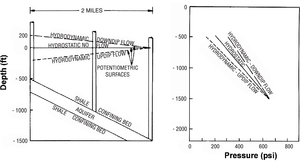
The potentiometric surface is the surface defined by the hydraulic head (elevation) from a rock unit from several different wells. If the potentiometric surface for a given subsurface rock unit is horizontal, then the potential energy of the water in that formation is constant and the water is at rest (hydrostatic). If the potentiometric surface is sloping, then the water moves (hydrodynamic) in the direction of the greatest downward slope.[1]
Figure 2 shows the potentiometric surface for hydrodynamic updip and downdip flow and hydrostatic no flow. The pressure-depth plot shows hypothetical pressure gradients for each condition.
See also
References
- ↑ 1.0 1.1 Hubbert, K., 1953, Entrapment of petroleum under hydrodynamic conditions: AAPG Bulletin, vol. 37, no. 8, p. 1954–2026. The original paper that proposed hydrodynamics as an important trapping mechanism.
- ↑ 2.0 2.1 Dahlberg, E. C., 1994, Applied Hydrodynamics in Petroleum Exploration, 2nd ed.: New York, Springer-Verlag, 295 p. Excellent subsurface fluid pressure reference. Covers hydrodynamic and static fluids.
- ↑ Schowalter, T. T., 1979, Mechanics of secondary hydrocarbon migration and entrapment: AAPG Bulletin, vol. 63, no. 5, p. 723–760. Covers many fluid behavior principles, including pressure, with broad application to petroleum exploration.

