Difference between revisions of "Hydrodynamic influence on trapping"
Jump to navigation
Jump to search
Cwhitehurst (talk | contribs) |
Cwhitehurst (talk | contribs) m (added Category:Treatise Handbook 3 using HotCat) |
||
| (8 intermediate revisions by 2 users not shown) | |||
| Line 6: | Line 6: | ||
| part = Critical elements of the petroleum system | | part = Critical elements of the petroleum system | ||
| chapter = Formation fluid pressure and its application | | chapter = Formation fluid pressure and its application | ||
| − | | frompg = 5- | + | | frompg = 5-60 |
| − | | topg = 5- | + | | topg = 5-60 |
| author = Edward A. Beaumont, Forrest Fiedler | | author = Edward A. Beaumont, Forrest Fiedler | ||
| link = http://archives.datapages.com/data/specpubs/beaumont/ch05/ch05.htm | | link = http://archives.datapages.com/data/specpubs/beaumont/ch05/ch05.htm | ||
| Line 18: | Line 18: | ||
===Potential of water vs. hydrocarbons=== | ===Potential of water vs. hydrocarbons=== | ||
| − | Fluid pressure equals | + | Fluid pressure equals ρgH. Under hydrostatic conditions, the buoyant force equals |
:<math>\rho_{\rm w} \mbox{gH}_{\rm w} - \rho_{\rm h}\mbox{gH}_{\rm h}</math> | :<math>\rho_{\rm w} \mbox{gH}_{\rm w} - \rho_{\rm h}\mbox{gH}_{\rm h}</math> | ||
| Line 25: | Line 25: | ||
* ρ<sub>w</sub> = water density | * ρ<sub>w</sub> = water density | ||
| − | * ρ<sub>h</sub> = hydrocarbon density | + | * ρ<sub>h</sub> = [[hydrocarbon]] density |
* H<sub>w</sub> = water depth | * H<sub>w</sub> = water depth | ||
| − | * H<sub>h</sub> = hydrocarbon column height | + | * H<sub>h</sub> = [[hydrocarbon column]] height |
Under hydrodynamic conditions, the potential for a hydrocarbon column (Φ<sub>h</sub>) is related to the potential of the water by the equation | Under hydrodynamic conditions, the potential for a hydrocarbon column (Φ<sub>h</sub>) is related to the potential of the water by the equation | ||
| Line 33: | Line 33: | ||
:<math>\Phi_{\rm h} = \rho_{\rm h}\mbox{gH}_{\rm h} = \rho_{\rm w}\mbox{gH}_{\rm w} - (\rho_{\rm w} - \rho_{\rm h})\mbox{gZ}</math> | :<math>\Phi_{\rm h} = \rho_{\rm h}\mbox{gH}_{\rm h} = \rho_{\rm w}\mbox{gH}_{\rm w} - (\rho_{\rm w} - \rho_{\rm h})\mbox{gZ}</math> | ||
| − | Dividing through by g (ρ<sub>w</sub> – ρ<sub>h</sub>)/ρ<sub>h</sub> to simplify gives (in a uniformly flat gravity field) | + | Dividing through by g (ρ<sub>w</sub> – ρ<sub>h</sub>)/ρ<sub>h</sub> to simplify gives (in a uniformly flat [[gravity]] field) |
:<math>\left(\frac{\rho_{\rm h}}{\rho_{\rm w} - \rho_{\rm h}}\right) \mbox{H}_{\rm h} = \left(\frac{\rho_{\rm w}}{\rho_{\rm w} - \rho_{\rm h}}\right)\mbox{H}_{\rm w} - \mbox{Z}</math> | :<math>\left(\frac{\rho_{\rm h}}{\rho_{\rm w} - \rho_{\rm h}}\right) \mbox{H}_{\rm h} = \left(\frac{\rho_{\rm w}}{\rho_{\rm w} - \rho_{\rm h}}\right)\mbox{H}_{\rm w} - \mbox{Z}</math> | ||
| − | Constant values for the left-hand side of the equation are equipotential surfaces for hydrocarbons. Hubbert<ref name=ch05r11>Hubbert, K., 1953, [http://archives.datapages.com/data/bulletns/1953-56/data/pg/0037/0008/1950/1954.htm Entrapment of petroleum under hydrodynamic conditions]: AAPG Bulletin, vol. 37, no. 8, p. 1954–2026. The original paper that proposed hydrodynamics as an important trapping mechanism.</ref> called this factor U. From the right side, constant values for ρ<sub>w</sub>/(ρ<sub>w</sub> – ρ<sub>h</sub>)H<sub>w</sub> are equipotential surfaces for water. Hubbert called this factor V. The elevation factor (Z) is the difference between the equipotential surfaces for hydrocarbons and water. | + | Constant values for the left-hand side of the equation are [[Wikipedia:Equipotential|equipotential]] surfaces for hydrocarbons. Hubbert<ref name=ch05r11>Hubbert, K., 1953, [http://archives.datapages.com/data/bulletns/1953-56/data/pg/0037/0008/1950/1954.htm Entrapment of petroleum under hydrodynamic conditions]: AAPG Bulletin, vol. 37, no. 8, p. 1954–2026. The original paper that proposed hydrodynamics as an important trapping mechanism.</ref> called this factor U. From the right side, constant values for ρ<sub>w</sub>/(ρ<sub>w</sub> – ρ<sub>h</sub>)H<sub>w</sub> are equipotential surfaces for water. Hubbert called this factor V. The elevation factor (Z) is the difference between the equipotential surfaces for hydrocarbons and water. |
Substituting U and V in the above equation gives | Substituting U and V in the above equation gives | ||
| Line 47: | Line 47: | ||
===Hydrodynamic effect on traps=== | ===Hydrodynamic effect on traps=== | ||
| − | [[file:formation-fluid-pressure-and-its-application_fig5-37.png|300px|thumb|{{figure number|1}}Vectors and equipotential lines for a hydrocarbon accumulation in an anticline in a hydrodynamic environment. Modified. Copyright: North, 1985 | + | [[file:formation-fluid-pressure-and-its-application_fig5-37.png|300px|thumb|{{figure number|1}}Vectors and equipotential lines for a hydrocarbon accumulation in an anticline in a hydrodynamic environment. Modified. Copyright: North;<ref name=North1985>North, F. K., 1985, Petroleum Geology: London, Allen & Unwin, 246 p.</ref> courtesy Allen and Unwin.]] |
| − | In a hydrostatic environment, the free-water level of a trap is horizontal. In a hydrodynamic environment, the free-water level of a trap is tilted because the buoyant force (P<sub>b</sub>) is interfered with by the hydrodynamic force (P<sub>w</sub>). The resultant interference is the vector known as the confining force (P<sub>cf</sub>). U, an equipotential line, is perpendicular to P<sub>cf</sub> and is tilted because of the effect of P<sub>w</sub>. The diagram in [[:file:formation-fluid-pressure-and-its-application_fig5-37.png|Figure 1]] shows these vectors and the equipotential lines for a hydrocarbon accumulation in an anticline in a hydrodynamic environment. | + | In a hydrostatic environment, the free-water level of a trap is horizontal. In a hydrodynamic environment, the free-water level of a trap is tilted because the buoyant force (P<sub>b</sub>) is interfered with by the hydrodynamic force (P<sub>w</sub>). The resultant interference is the vector known as the confining force (P<sub>cf</sub>). U, an equipotential line, is perpendicular to P<sub>cf</sub> and is tilted because of the effect of P<sub>w</sub>. The diagram in [[:file:formation-fluid-pressure-and-its-application_fig5-37.png|Figure 1]] shows these vectors and the equipotential lines for a hydrocarbon [[accumulation]] in an [[anticline]] in a hydrodynamic environment. |
==See also== | ==See also== | ||
| Line 65: | Line 65: | ||
[[Category:Critical elements of the petroleum system]] | [[Category:Critical elements of the petroleum system]] | ||
[[Category:Formation fluid pressure and its application]] | [[Category:Formation fluid pressure and its application]] | ||
| + | [[Category:Treatise Handbook 3]] | ||
Latest revision as of 22:08, 17 February 2022
| Exploring for Oil and Gas Traps | |
| |
| Series | Treatise in Petroleum Geology |
|---|---|
| Part | Critical elements of the petroleum system |
| Chapter | Formation fluid pressure and its application |
| Author | Edward A. Beaumont, Forrest Fiedler |
| Link | Web page |
| Store | AAPG Store |
Hydrodynamic influence on trapping
Potential of water vs. hydrocarbons
Fluid pressure equals ρgH. Under hydrostatic conditions, the buoyant force equals
where:
- ρw = water density
- ρh = hydrocarbon density
- Hw = water depth
- Hh = hydrocarbon column height
Under hydrodynamic conditions, the potential for a hydrocarbon column (Φh) is related to the potential of the water by the equation
Dividing through by g (ρw – ρh)/ρh to simplify gives (in a uniformly flat gravity field)
Constant values for the left-hand side of the equation are equipotential surfaces for hydrocarbons. Hubbert[1] called this factor U. From the right side, constant values for ρw/(ρw – ρh)Hw are equipotential surfaces for water. Hubbert called this factor V. The elevation factor (Z) is the difference between the equipotential surfaces for hydrocarbons and water.
Substituting U and V in the above equation gives
Fluid flow is perpendicular to equipotential surfaces.
Hydrodynamic effect on traps
Figure 1 Vectors and equipotential lines for a hydrocarbon accumulation in an anticline in a hydrodynamic environment. Modified. Copyright: North;[2] courtesy Allen and Unwin.
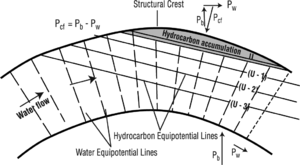
In a hydrostatic environment, the free-water level of a trap is horizontal. In a hydrodynamic environment, the free-water level of a trap is tilted because the buoyant force (Pb) is interfered with by the hydrodynamic force (Pw). The resultant interference is the vector known as the confining force (Pcf). U, an equipotential line, is perpendicular to Pcf and is tilted because of the effect of Pw. The diagram in Figure 1 shows these vectors and the equipotential lines for a hydrocarbon accumulation in an anticline in a hydrodynamic environment.
See also
References
- ↑ Hubbert, K., 1953, Entrapment of petroleum under hydrodynamic conditions: AAPG Bulletin, vol. 37, no. 8, p. 1954–2026. The original paper that proposed hydrodynamics as an important trapping mechanism.
- ↑ North, F. K., 1985, Petroleum Geology: London, Allen & Unwin, 246 p.
External links
| find literature about Hydrodynamic influence on trapping |
|
|
|
|