Difference between revisions of "Structural restoration"
Cwhitehurst (talk | contribs) |
Cwhitehurst (talk | contribs) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
|Competition=[[2021 Middle East Wiki Write Off]] | |Competition=[[2021 Middle East Wiki Write Off]] | ||
}} | }} | ||
| − | In structural geology, restoration is the process of reversing rock deformation in the subsurface through time, which can be achieved by using modeling techniques (e.g., kinematic, geometrical, and geomechanical). For instance, seismic sections from an area of interest can be used to generate restored seismic cross sections to illustrate past subsurface geology.<ref | + | In structural geology, restoration is the process of reversing rock deformation in the subsurface through time, which can be achieved by using modeling techniques (e.g., kinematic, geometrical, and geomechanical). For instance, seismic sections from an area of interest can be used to generate restored seismic cross sections to illustrate past subsurface geology.<ref>Nunns, A. G., 1991, Structural restoration of seismic and geologic sections in extensional regimes: AAPG Bulletin, v. 75, no. 2, p. 278-297.</ref> |
==Background== | ==Background== | ||
| − | Structural restoration is a collective term that encompasses several methods used to reverse the history of deformation and yield a pre-deformational state of the area in a single step restoration or in several intermediate stages (sequential restoration).<ref | + | Structural restoration is a collective term that encompasses several methods used to reverse the history of deformation and yield a pre-deformational state of the area in a single step restoration or in several intermediate stages (sequential restoration).<ref>Vidal-Royo, O., T. E. Hearon IV, C. D. Connors, S. Bland, F. Schaefer, O. Ferrer, I. Mora, et al., 2015, Introduction to special section: Balancing, restoration, and palinspastic reconstruction: Intrepretation, v. 3 no. 4, p. 1N-Y1</ref> Structural restoration is linked to structural balancing, which is the adjustment of geological interpretation – of a section or an area – so that mass conservation before and after the strain is maintained. Therefore, a balanced section should be: |
# accurate, | # accurate, | ||
# geologically admissible, | # geologically admissible, | ||
# restorable (it should be possible to return the section to a pre-deformation geometry), | # restorable (it should be possible to return the section to a pre-deformation geometry), | ||
| − | # balanced/valid (mass conservation is maintained).<ref name= | + | # balanced/valid (mass conservation is maintained).<ref name=Dahlstrom>Dahlstrom, C. D. A., 1969, Balanced cross sections: Canadian Journal of Earth Sciences, v. 6, no. 4, p. 743-757.</ref><ref name=Elliott>Elliott, D., 1983, The construction of balanced cross-sections: Journal of Structural Geology, v. 5, no. 2, p. 101.</ref> |
Therefore, structural balancing represents a powerful tool to predict unseen, subsurface geometries based on input data (e.g., outcrop geometries, well-imaged seismic sections/volumes, etc.) | Therefore, structural balancing represents a powerful tool to predict unseen, subsurface geometries based on input data (e.g., outcrop geometries, well-imaged seismic sections/volumes, etc.) | ||
==History== | ==History== | ||
| − | Structural balancing was first applied (but not introduced as a term) by Chamberlin<ref name=Chamberlin_1910>Chamberlin, R. T., 1910, The Appalachian folds of central Pennsylvania: The Journal of Geology, v. 18, no. 3, p. 228-251.</ref> to predict the geometry of the subsurface based on outcrop relationships. At the start of the | + | Structural balancing was first applied (but not introduced as a term) by Chamberlin<ref name=Chamberlin_1910>Chamberlin, R. T., 1910, The Appalachian folds of central Pennsylvania: The Journal of Geology, v. 18, no. 3, p. 228-251.</ref> to predict the geometry of the subsurface based on outcrop relationships. At the start of the twentieth century, deciphering the evolution of mountain belts and orogens represented an early stage of studying the kinematics associated with deformation.<ref name=Peach>Peach, B. N., J. Horne, W. Gunn, C. T. Clough, and L. W. Hinxman, 1907, The geological structure of the North-West Highlands of Scotland: Glasgow, Scotland, HM Stationery Office, 668 p.</ref> As a defined term, balancing initially referred to the conservation of bed lengths and thicknesses.<ref name=Dahlstrom /> |
| − | In the 1960s, Bally et al.<ref | + | In the 1960s, Bally et al.<ref>Bally, A. W., P. L. Gordy, and G. A. Stewart, 1966, Structure, seismic data, and orogenic evolution of southern Canadian Rocky Mountains: Bulletin of Canadian Petroleum Geology, v. 14, no, 3, p. 337-381.</ref> and Dahlstrom<ref name=Dahlstrom /> first used restoration as a tool to assess interpretation and predict geometry of structures whose interpretations were highly uncertain. Advancements in computer science at the end of the century has had great impact in converting balancing and restoration concepts into software applications that can handle structural analysis of 2-D sections and maps. Most recently as computer power increased and algorithms enhanced, commercial software applications allowed for the handling of 3-D volumes balancing and restoration. |
==Rationale and theory== | ==Rationale and theory== | ||
| − | Understanding the underlying geology of sedimentary basins is often hindered by the existence of complex structures and/or lack of data, leading to highly uncertain models, and thus exploration/operational difficulties. For that, subsurface dynamic structural models are critical for constructing an understanding of the structural evolution of a basin of interest. For instance, tectonic controls such as faults and subsidence/uplift play a significant role in altering the subsurface geology, impacting petroleum system elements such as reservoir distribution and source rock burial depth. Dynamic restoration models as such can aid the understanding of petroleum systems processes, including hydrocarbon maturation, expulsion, migration and accumulation, and potentially present-day location of hydrocarbon fields.<ref name=Neumaier_2016>Neumaier, M. | + | Understanding the underlying geology of sedimentary basins is often hindered by the existence of complex structures and/or lack of data, leading to highly uncertain models, and thus exploration/operational difficulties. For that, subsurface dynamic structural models are critical for constructing an understanding of the structural evolution of a basin of interest. For instance, tectonic controls such as faults and subsidence/uplift play a significant role in altering the subsurface geology, impacting petroleum system elements such as reservoir distribution and source rock burial depth. Dynamic restoration models as such can aid the understanding of petroleum systems processes, including hydrocarbon maturation, expulsion, migration and accumulation, and potentially present-day location of hydrocarbon fields.<ref name=Neumaier_2016>Neumaier, M., 2016, Structural restoration and basin and petroleum systems modeling: Case studies from the Monagas Fold and Thrust Belt, Venezuela and the Moroccan Atlantic Margin: Doctoral dissertation, Universitätsbibliothek der RWTH Aachen.</ref> Structural balancing and restoration combined make a good tool that can be used to validate structural models and predict untapped locations with more confidence in a geologically plausible manner. |
| − | [[file:AlHawajAlQahtaniFigure1.jpg|center|framed|{{figure number|1}} | + | [[file:AlHawajAlQahtaniFigure1.jpg|center|framed|{{figure number|1}}3-D restoration conducted on a faulted and folded layer (Sub-Andean Zone, Bolivia), showing a) the deformed state and b) the restored state. c) Distribution of maximum principal stress that resulted from the deformation in a.<ref name=Morettietal_2006>Moretti, I., F. Lepage, and M. Guiton, 2006, KINE3D: A new 3D restoration method based on a mixed approach linking geometry and geomechanics: Oil & Gas Science and Technology, v. 61. no. 2, p. 277-289.</ref>]] |
Structural restoration can be conducted in 2-D and 3D models. As 3-D applications help to quantify spatial distribution of deformation, 2D balancing and restoration can be used to validate interpretation at parts of the volume of interest, which can be edited before committing to the 3-D workflow ([[:file:AlHawajAlQahtaniFigure1.jpg|Figure 1]]). | Structural restoration can be conducted in 2-D and 3D models. As 3-D applications help to quantify spatial distribution of deformation, 2D balancing and restoration can be used to validate interpretation at parts of the volume of interest, which can be edited before committing to the 3-D workflow ([[:file:AlHawajAlQahtaniFigure1.jpg|Figure 1]]). | ||
| Line 30: | Line 30: | ||
* Geometric Methods: Geometric balancing strives to balance one or more aspects of the geometry (e.g. horizon length, formation cross-sectional area). | * Geometric Methods: Geometric balancing strives to balance one or more aspects of the geometry (e.g. horizon length, formation cross-sectional area). | ||
* Kinematic Modeling: Balancing and restoration utilize concepts of deformation kinematics and dynamics that are best visualized in forward modeling. Kinematic modeling reproduces the structural geometry as the structure moves (i.e. geometry-based kinematic models). | * Kinematic Modeling: Balancing and restoration utilize concepts of deformation kinematics and dynamics that are best visualized in forward modeling. Kinematic modeling reproduces the structural geometry as the structure moves (i.e. geometry-based kinematic models). | ||
| − | * Numerical Modeling: Numerical modeling provides a great advancement over geometric models whereby the physical properties of the formations can be modeled during the deformation. An example of such development in 2D modeling of fault-propagation folds is the trishear model that incorporates not only the strain in the hanging wall block but also that in the footwall block.<ref | + | * Numerical Modeling: Numerical modeling provides a great advancement over geometric models whereby the physical properties of the formations can be modeled during the deformation. An example of such development in 2D modeling of fault-propagation folds is the trishear model that incorporates not only the strain in the hanging wall block but also that in the footwall block.<ref>Erslev, E. A., 1991, Trishear fault-propagation folding: Geology, v. 19, no. 6, p. 617-620.</ref> Three-dimensional trishear modeling followed after at the beginning of the 21st century.<ref>Cristallini, E. O., L. Giambiagi, and R. W. Allmendinger, 2004, True three-dimensional trishear: A kinematic model for strike-slip and oblique-slip deformation: Geological Society of America Bulletin, v. 116, no. 7-8, p. 938-952.</ref> |
* Geomechanical Modeling: Geomechanical modeling covers not only the geometric aspects but also the states of stress and strain that caused and accompanied the deformation by using, boundary, discrete and finite element modeling.<ref name=Masinietal_2011>Masini, M., S. Bigi, J., Poblet, M. Bulnes, R. Di Cuia, and D. Casabianca, 2011, Kinematic evolution and strain simulation, based on cross-section restoration, of the Maiella Mountain: An analogue for oil fields in the Apennines (Italy), ''in'' J. Poblet and R. J. Lisle, eds., Kinematic evolution and structural styles of fold-and-thrust belts: Geological Society (London) Special Publication 349, p. 25-44.</ref> | * Geomechanical Modeling: Geomechanical modeling covers not only the geometric aspects but also the states of stress and strain that caused and accompanied the deformation by using, boundary, discrete and finite element modeling.<ref name=Masinietal_2011>Masini, M., S. Bigi, J., Poblet, M. Bulnes, R. Di Cuia, and D. Casabianca, 2011, Kinematic evolution and strain simulation, based on cross-section restoration, of the Maiella Mountain: An analogue for oil fields in the Apennines (Italy), ''in'' J. Poblet and R. J. Lisle, eds., Kinematic evolution and structural styles of fold-and-thrust belts: Geological Society (London) Special Publication 349, p. 25-44.</ref> | ||
| Line 68: | Line 68: | ||
The impact of structural restoration on petroleum exploration and development resides in its ability to evaluate the relative timing of petroleum system elements and processes. In particular, structural restoration constrains the timing of these elements, which helps to de-risk them when evaluating a prospect. Of particular importance is the timing of the trap formation that can be evaluated using structural restoration and compared to the timing of the hydrocarbon expulsion and migration. For example, [[:file:AlHawajAlQahtaniFigure4.jpg|Figure 4]] shows 2D geological evolution at the Monagas Fold and Thrust Belt in Venezuela, demonstrating the temporal relationship between trap formation and source rock maturation and hydrocarbon expulsion, migration, and accumulation in a structurally complex basin.<ref name=Neumaier_2016 /> | The impact of structural restoration on petroleum exploration and development resides in its ability to evaluate the relative timing of petroleum system elements and processes. In particular, structural restoration constrains the timing of these elements, which helps to de-risk them when evaluating a prospect. Of particular importance is the timing of the trap formation that can be evaluated using structural restoration and compared to the timing of the hydrocarbon expulsion and migration. For example, [[:file:AlHawajAlQahtaniFigure4.jpg|Figure 4]] shows 2D geological evolution at the Monagas Fold and Thrust Belt in Venezuela, demonstrating the temporal relationship between trap formation and source rock maturation and hydrocarbon expulsion, migration, and accumulation in a structurally complex basin.<ref name=Neumaier_2016 /> | ||
| − | + | ||
==Challenges== | ==Challenges== | ||
One of the main challenges encountered during restoration is the three-dimensional nature of geology, which means that out-of-plane deformation may not be captured by the conventional 2D section restoration. This is most obvious when trying to restore salt basins or blocks affected by strike-slip deformation. | One of the main challenges encountered during restoration is the three-dimensional nature of geology, which means that out-of-plane deformation may not be captured by the conventional 2D section restoration. This is most obvious when trying to restore salt basins or blocks affected by strike-slip deformation. | ||
| − | |||
| − | + | <gallery mode=packed style=center heights=400px> | |
| + | file:AlHawajAlQahtaniFigure5.jpg|{{figure number|5}}Schematic 3D geometry of salt structures rising from a) line sources and b) point sources. Note the complexity in all directions resulting from salt deformation.<ref name=HudecandJackson_2007>Hudec, M. R., and M. P. Jackson, 2007, Terra infirma: Understanding salt tectonics: Earth-Science Reviews, v. 82, no. 1-2, p. 1-28.</ref> | ||
| + | file:AlHawajAlQahtaniFigure6.jpg|{{figure number|6}}Examples from the deep-water Niger Delta of using channel geometry to constrain strike-slip displacement.<ref name=Durandriardetal_2013>Durand-Riard, P., J. H. Shaw, A., Plesch, and G. Lufadeju, 2013, Enabling 3-D geomechanical restoration of strike-and oblique-slip faults using geological constraints, with applications to the deep-water Niger Delta: Journal of Structural Geology, v. 48, p. 33-44.</ref> A) Faulted horizon surface. The small black box is the location of B-E. B-D) Channels lateral geometry on different horizon levels. E) Restoration using the channels geometry to constrain strike-slip displacement. F) Faulted horizon surface. The small black box is the location of G & H. G) Channels lateral geometry on different horizon levels. H) Restored state. | ||
| + | </gallery> | ||
| + | |||
| + | ===Salt tectonics=== | ||
| + | The underlying cause for the complexity in deformation in salt basins is that salt rock can flow in different directions that are not necessarily perpendicular to the basin margin when subjected to burial, compaction and margin tilt ([[:file:AlHawajAlQahtaniFigure5.jpg|Figure 5]]).<ref name=Fossen_2016>Fossen, H. (2016). Structural geology. Cambridge university press.</ref> When such flow is out-of-plane with respect to a cross section, performing 2-D balancing would most likely not yield conserved cross-sectional areas of the salt and, therefore, restoration may not be adequate. This necessitates the use of 3D restoration to better restore deformation in salt basins in the regional scale and validate the results of the 2-D restoration.<ref>Rowan, M. G., and R. A. Ratliff, 2012, Cross-section restoration of salt-related deformation: Best practices and potential pitfalls: Journal of Structural Geology, v. 41, p. 24-37.</ref> | ||
| − | + | ===Strike-slip tectonics=== | |
| + | The out-of-plane transport direction also affects the 2D restoration of areas affected by strike-slip faults. Furthermore, the limited dip-slip component in most strike-slip faults means that flattening of younger strata to estimate displacement and perform the restoration will most likely not yield fully restored sections/volumes.<ref name=Durandriardetal_2013 /> Hence, it is advised that features that have certain spatial geometry (e.g. channels, older faults) and are cut by the strike-slip fault be used to put constraint on the horizontal displacement. [[:file:AlHawajAlQahtaniFigure6.jpg|Figure 6]] shows an example from the deep-water Niger Delta where 3D geomechanical restoration of strike-slip faults was enabled by utilizing such lateral constraints.<ref name=Peach /> | ||
==See also== | ==See also== | ||
Latest revision as of 17:14, 13 October 2022
| Wiki Write-Off Entry | |
|---|---|

| |
| Author | Ahmed Al Hawaj and Saleh Al Qahtani |
| Affiliation | Saudi Aramco |
| Competition | 2021 Middle East Wiki Write Off |
In structural geology, restoration is the process of reversing rock deformation in the subsurface through time, which can be achieved by using modeling techniques (e.g., kinematic, geometrical, and geomechanical). For instance, seismic sections from an area of interest can be used to generate restored seismic cross sections to illustrate past subsurface geology.[1]
Background
Structural restoration is a collective term that encompasses several methods used to reverse the history of deformation and yield a pre-deformational state of the area in a single step restoration or in several intermediate stages (sequential restoration).[2] Structural restoration is linked to structural balancing, which is the adjustment of geological interpretation – of a section or an area – so that mass conservation before and after the strain is maintained. Therefore, a balanced section should be:
- accurate,
- geologically admissible,
- restorable (it should be possible to return the section to a pre-deformation geometry),
- balanced/valid (mass conservation is maintained).[3][4]
Therefore, structural balancing represents a powerful tool to predict unseen, subsurface geometries based on input data (e.g., outcrop geometries, well-imaged seismic sections/volumes, etc.)
History
Structural balancing was first applied (but not introduced as a term) by Chamberlin[5] to predict the geometry of the subsurface based on outcrop relationships. At the start of the twentieth century, deciphering the evolution of mountain belts and orogens represented an early stage of studying the kinematics associated with deformation.[6] As a defined term, balancing initially referred to the conservation of bed lengths and thicknesses.[3]
In the 1960s, Bally et al.[7] and Dahlstrom[3] first used restoration as a tool to assess interpretation and predict geometry of structures whose interpretations were highly uncertain. Advancements in computer science at the end of the century has had great impact in converting balancing and restoration concepts into software applications that can handle structural analysis of 2-D sections and maps. Most recently as computer power increased and algorithms enhanced, commercial software applications allowed for the handling of 3-D volumes balancing and restoration.
Rationale and theory
Understanding the underlying geology of sedimentary basins is often hindered by the existence of complex structures and/or lack of data, leading to highly uncertain models, and thus exploration/operational difficulties. For that, subsurface dynamic structural models are critical for constructing an understanding of the structural evolution of a basin of interest. For instance, tectonic controls such as faults and subsidence/uplift play a significant role in altering the subsurface geology, impacting petroleum system elements such as reservoir distribution and source rock burial depth. Dynamic restoration models as such can aid the understanding of petroleum systems processes, including hydrocarbon maturation, expulsion, migration and accumulation, and potentially present-day location of hydrocarbon fields.[8] Structural balancing and restoration combined make a good tool that can be used to validate structural models and predict untapped locations with more confidence in a geologically plausible manner.
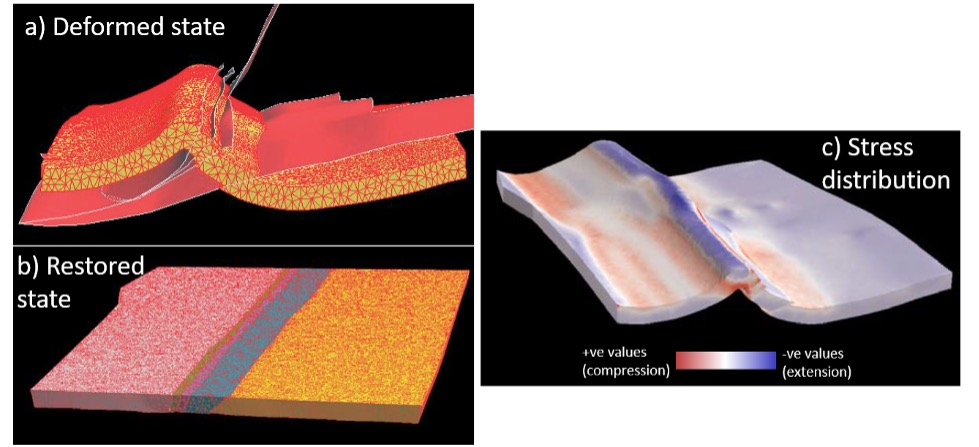
Structural restoration can be conducted in 2-D and 3D models. As 3-D applications help to quantify spatial distribution of deformation, 2D balancing and restoration can be used to validate interpretation at parts of the volume of interest, which can be edited before committing to the 3-D workflow (Figure 1).
Several established techniques have been used as a basis for restoration workflow, which are:
- Geometric Methods: Geometric balancing strives to balance one or more aspects of the geometry (e.g. horizon length, formation cross-sectional area).
- Kinematic Modeling: Balancing and restoration utilize concepts of deformation kinematics and dynamics that are best visualized in forward modeling. Kinematic modeling reproduces the structural geometry as the structure moves (i.e. geometry-based kinematic models).
- Numerical Modeling: Numerical modeling provides a great advancement over geometric models whereby the physical properties of the formations can be modeled during the deformation. An example of such development in 2D modeling of fault-propagation folds is the trishear model that incorporates not only the strain in the hanging wall block but also that in the footwall block.[10] Three-dimensional trishear modeling followed after at the beginning of the 21st century.[11]
- Geomechanical Modeling: Geomechanical modeling covers not only the geometric aspects but also the states of stress and strain that caused and accompanied the deformation by using, boundary, discrete and finite element modeling.[12]
Workflow
The proposed workflow focuses on using present-day depth-converted seismic interpretation and rock properties to perform backward-sequence restoration from the youngest to the oldest deposits and tectonic processes. After the integration of input data such as seismic interpretation and rock properties, and the generation of structural/geological model, the following is performed:
- decompaction (i.e., porosity/rock volume restoration),
- fault restoration,
- fold restoration and horizon flattening,
- uplift and subsidence restoration,
- restoration of eroded sections.
The validity of structural restoration is determined by achieving a dynamic restoration model that is both balanced and geologically plausible. It is worth pointing out that several dynamic restoration models may be considered valid. For that, it is recommended to test multiple restoration scenarios. Output results include paleotopography maps, quantified analysis of basin extension/compression, and stress/strain mapping and simulation. If the results are not valid, then seismic reinterpretation must be performed to regenerate an alternative structural/geological model. Figure 2 summarizes the proposed restoration steps.
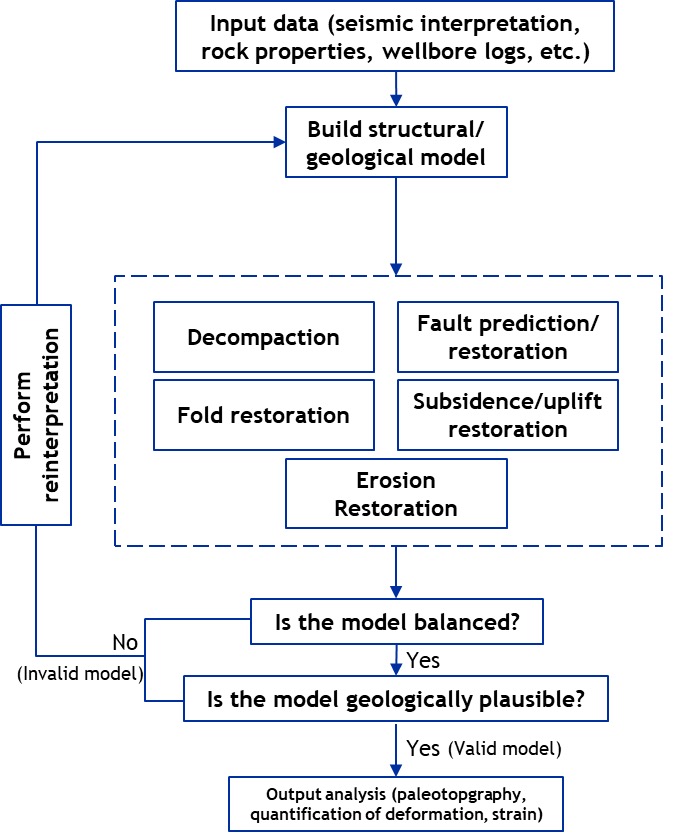
Restoration results
A number of results useful for a range of geological assessments can emerge from structural restoration. These include validation of interpretation, prediction of unseen structures and horizons geometries, estimation of extension and shortening, quantification of uplift and erosion, and construction of paleo-topographic and paleo-bathymetric maps. Additionally, restoration can be used to simulate geomechanical properties such as the distribution of stress and strain.
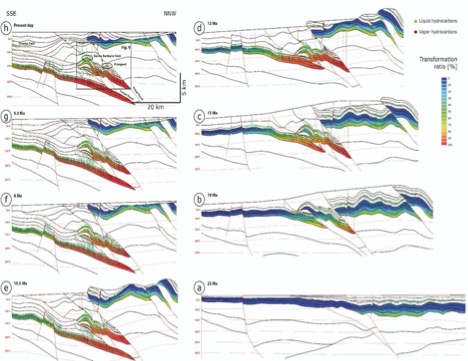
Figure 3 Examples of 2-D restoration at extensional (left) and compressional (right) regimes.[8]
Figure 4 Restoration steps on a 2-D section at the Monagas Fold and Thrust Belt (Venezuela) showing how and when traps formed with respect to the migration and accumulation of oil and gas.[8]
Validation/invalidation of interpretation and prediction of unseen geometries
Structural restoration and balancing assist in evaluating the interpretation, making them powerful tools in predicting the geometries of horizons and faults that are not imaged or only poorly imaged. In doing so, the interpreted faults and horizons are checked against geologically plausible deformational models and styles to test their viability. For instance, Chamberlin[5] used balancing methods to predict the geometry of the subsurface based on outcrop relationships.
Estimating extension, shortening and sub-seismic deformation
Balancing and restoration can be used to quantify the amount of extension and shortening by measuring the length difference between the deformed state and undeformed (restored) state (Figure 3). Additionally, restoration allows for the simulation of strain and dilatancy (Figure 2).
Estimation of uplift and erosion
Rock and surface uplifts can lead to erosion and non-deposition, which would result in the removal of previously deposited sections. This means that there will be a difference between the area/volume/line length of the restored and the deformed rock. The importance of balancing and restoration is that such dissimilarity can be pinpointed in space and time to reincorporate missing section/volume back into the geological evolution.
Paleotopography and paleobathymetry
Restoration, in particular 3-D restoration, can be used to generate paleo-surfaces that are geologically plausible given the data. These paleo-surfaces can be incorporated into basin- and prospect-scale modeling of, for example, GDEs. Such application is important where sediment pathways are greatly affected by evolving structures. Paleo-surfaces are also important for constraining and calibrating petroleum system models over the basin scale as they can be used as an input in basin modeling.
Example from industry
The impact of structural restoration on petroleum exploration and development resides in its ability to evaluate the relative timing of petroleum system elements and processes. In particular, structural restoration constrains the timing of these elements, which helps to de-risk them when evaluating a prospect. Of particular importance is the timing of the trap formation that can be evaluated using structural restoration and compared to the timing of the hydrocarbon expulsion and migration. For example, Figure 4 shows 2D geological evolution at the Monagas Fold and Thrust Belt in Venezuela, demonstrating the temporal relationship between trap formation and source rock maturation and hydrocarbon expulsion, migration, and accumulation in a structurally complex basin.[8]
Challenges
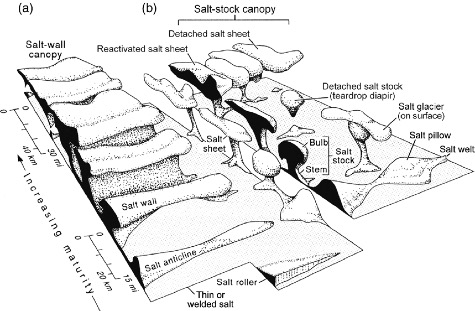
One of the main challenges encountered during restoration is the three-dimensional nature of geology, which means that out-of-plane deformation may not be captured by the conventional 2D section restoration. This is most obvious when trying to restore salt basins or blocks affected by strike-slip deformation.
Figure 5 Schematic 3D geometry of salt structures rising from a) line sources and b) point sources. Note the complexity in all directions resulting from salt deformation.[14]
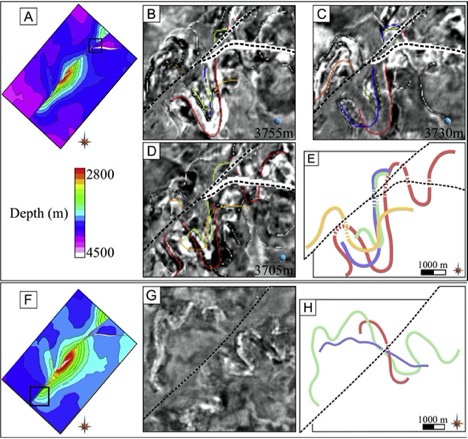
Figure 6 Examples from the deep-water Niger Delta of using channel geometry to constrain strike-slip displacement.[15] A) Faulted horizon surface. The small black box is the location of B-E. B-D) Channels lateral geometry on different horizon levels. E) Restoration using the channels geometry to constrain strike-slip displacement. F) Faulted horizon surface. The small black box is the location of G & H. G) Channels lateral geometry on different horizon levels. H) Restored state.
Salt tectonics
The underlying cause for the complexity in deformation in salt basins is that salt rock can flow in different directions that are not necessarily perpendicular to the basin margin when subjected to burial, compaction and margin tilt (Figure 5).[16] When such flow is out-of-plane with respect to a cross section, performing 2-D balancing would most likely not yield conserved cross-sectional areas of the salt and, therefore, restoration may not be adequate. This necessitates the use of 3D restoration to better restore deformation in salt basins in the regional scale and validate the results of the 2-D restoration.[17]
Strike-slip tectonics
The out-of-plane transport direction also affects the 2D restoration of areas affected by strike-slip faults. Furthermore, the limited dip-slip component in most strike-slip faults means that flattening of younger strata to estimate displacement and perform the restoration will most likely not yield fully restored sections/volumes.[15] Hence, it is advised that features that have certain spatial geometry (e.g. channels, older faults) and are cut by the strike-slip fault be used to put constraint on the horizontal displacement. Figure 6 shows an example from the deep-water Niger Delta where 3D geomechanical restoration of strike-slip faults was enabled by utilizing such lateral constraints.[6]
See also
- 2021 Middle East Wiki Write Off
- Fault seal analysis for reservoir development
- Super basins
- Condensate banking effect
References
- ↑ Nunns, A. G., 1991, Structural restoration of seismic and geologic sections in extensional regimes: AAPG Bulletin, v. 75, no. 2, p. 278-297.
- ↑ Vidal-Royo, O., T. E. Hearon IV, C. D. Connors, S. Bland, F. Schaefer, O. Ferrer, I. Mora, et al., 2015, Introduction to special section: Balancing, restoration, and palinspastic reconstruction: Intrepretation, v. 3 no. 4, p. 1N-Y1
- ↑ 3.0 3.1 3.2 Dahlstrom, C. D. A., 1969, Balanced cross sections: Canadian Journal of Earth Sciences, v. 6, no. 4, p. 743-757.
- ↑ Elliott, D., 1983, The construction of balanced cross-sections: Journal of Structural Geology, v. 5, no. 2, p. 101.
- ↑ 5.0 5.1 Chamberlin, R. T., 1910, The Appalachian folds of central Pennsylvania: The Journal of Geology, v. 18, no. 3, p. 228-251.
- ↑ 6.0 6.1 Peach, B. N., J. Horne, W. Gunn, C. T. Clough, and L. W. Hinxman, 1907, The geological structure of the North-West Highlands of Scotland: Glasgow, Scotland, HM Stationery Office, 668 p.
- ↑ Bally, A. W., P. L. Gordy, and G. A. Stewart, 1966, Structure, seismic data, and orogenic evolution of southern Canadian Rocky Mountains: Bulletin of Canadian Petroleum Geology, v. 14, no, 3, p. 337-381.
- ↑ 8.0 8.1 8.2 8.3 Neumaier, M., 2016, Structural restoration and basin and petroleum systems modeling: Case studies from the Monagas Fold and Thrust Belt, Venezuela and the Moroccan Atlantic Margin: Doctoral dissertation, Universitätsbibliothek der RWTH Aachen.
- ↑ Moretti, I., F. Lepage, and M. Guiton, 2006, KINE3D: A new 3D restoration method based on a mixed approach linking geometry and geomechanics: Oil & Gas Science and Technology, v. 61. no. 2, p. 277-289.
- ↑ Erslev, E. A., 1991, Trishear fault-propagation folding: Geology, v. 19, no. 6, p. 617-620.
- ↑ Cristallini, E. O., L. Giambiagi, and R. W. Allmendinger, 2004, True three-dimensional trishear: A kinematic model for strike-slip and oblique-slip deformation: Geological Society of America Bulletin, v. 116, no. 7-8, p. 938-952.
- ↑ Masini, M., S. Bigi, J., Poblet, M. Bulnes, R. Di Cuia, and D. Casabianca, 2011, Kinematic evolution and strain simulation, based on cross-section restoration, of the Maiella Mountain: An analogue for oil fields in the Apennines (Italy), in J. Poblet and R. J. Lisle, eds., Kinematic evolution and structural styles of fold-and-thrust belts: Geological Society (London) Special Publication 349, p. 25-44.
- ↑ Petroleum Experts. (2018). Best practices in 2D sequential restoration - Part 2. Edinburgh, Scotland, UK.
- ↑ Hudec, M. R., and M. P. Jackson, 2007, Terra infirma: Understanding salt tectonics: Earth-Science Reviews, v. 82, no. 1-2, p. 1-28.
- ↑ 15.0 15.1 Durand-Riard, P., J. H. Shaw, A., Plesch, and G. Lufadeju, 2013, Enabling 3-D geomechanical restoration of strike-and oblique-slip faults using geological constraints, with applications to the deep-water Niger Delta: Journal of Structural Geology, v. 48, p. 33-44.
- ↑ Fossen, H. (2016). Structural geology. Cambridge university press.
- ↑ Rowan, M. G., and R. A. Ratliff, 2012, Cross-section restoration of salt-related deformation: Best practices and potential pitfalls: Journal of Structural Geology, v. 41, p. 24-37.