Difference between revisions of "Borehole gravity tool"
Jump to navigation
Jump to search
FWhitehurst (talk | contribs) |
Cwhitehurst (talk | contribs) m (added Category:Treatise Handbook 3 using HotCat) |
||
| (12 intermediate revisions by 2 users not shown) | |||
| Line 15: | Line 15: | ||
}} | }} | ||
==How the tool measures gravity== | ==How the tool measures gravity== | ||
| + | |||
| + | [[file:applying-gravity-in-petroleum-exploration_fig15-10.png|300px|thumb|{{figure number|1}}Fundamentals of measuring density using a borehole gravity sensor. From Schowalter;<ref name=Schowalter1979>Schowalter, T. T., 1979, [http://archives.datapages.com/data/bulletns/1977-79/data/pg/0063/0005/0700/0723.htm Mechanics of secondary hydrocarbon migration and entrapment]: AAPG Bulletin, vol. 63, no. 5, p. 723–760.</ref> courtesy AAPG.]] | ||
[[:file:applying-gravity-in-petroleum-exploration_fig15-10.png|Figure 1]] illustrates the fundamentals of measuring density using a [[borehole gravity]] sensor. Two gravity measurements, ''g''<sub>1</sub> and ''g''<sub>2</sub>, are made downhole, separated in depth by Δ''z''. The value ''G'' is the universal gravity constant. Thus, the gravity gradient, Δ''g''/Δ''z'', is related directly to the density of the intervening layer. The result is a direct computation of the bulk density of that layer. | [[:file:applying-gravity-in-petroleum-exploration_fig15-10.png|Figure 1]] illustrates the fundamentals of measuring density using a [[borehole gravity]] sensor. Two gravity measurements, ''g''<sub>1</sub> and ''g''<sub>2</sub>, are made downhole, separated in depth by Δ''z''. The value ''G'' is the universal gravity constant. Thus, the gravity gradient, Δ''g''/Δ''z'', is related directly to the density of the intervening layer. The result is a direct computation of the bulk density of that layer. | ||
| − | + | ==Depth of investigation== | |
| − | [[file:applying-gravity-in-petroleum-exploration_fig15-11.png|thumb|{{figure number|2}}After .<ref name=ch15r9>McCulloh, T. | + | [[file:applying-gravity-in-petroleum-exploration_fig15-11.png|300px|thumb|{{figure number|2}}Depth of investigation is tunable by means of varying the separation between two gravity measurements, Δ''z''. After McCulloh et al.<ref name=ch15r9>McCulloh, T. H., J. R. Kandle, J. E. Schoellhamer, 1968, Application of gravity measurements in wells to problems of reservoir evaluation: Transactions of the 9th Annual SPWLA Logging Symposium. Fundamental work describing the distance of sources seen by the borehole gravity meter.</ref> Copyright: SPWLA.]] |
| − | + | [[:file:applying-gravity-in-petroleum-exploration_fig15-11.png|Figure 2]] shows how the depth of investigation is tunable by means of varying the separation between two [[gravity]] measurements, Δ''z''. The rule of thumb is that 90% of the gravity effect can be imaged at a distance away from the borehole within five times Δ''z''. | |
| − | [[:file:applying-gravity-in-petroleum-exploration_fig15-11.png|Figure 2]] shows how the depth of investigation is tunable by means of varying the separation between two gravity measurements, Δ''z''. The rule of thumb is that 90% of the gravity effect can be imaged at a distance away from the borehole within five times Δ''z''. | ||
==Depth of investigation of various logging methods== | ==Depth of investigation of various logging methods== | ||
| − | The following table, based on data from Beyer<ref name=ch15r1>Beyer, L. | + | The following table, based on data from Beyer<ref name=ch15r1>Beyer, L. A., 1991, [[Borehole gravity]] Surveys: SEG Short Course notes, June, 350 p.</ref> shows conservative estimates of the depth of investigation using various density logging tools. [[Borehole gravity]] can sample the farthest distance and investigate the most formation. |
{| class = "wikitable" | {| class = "wikitable" | ||
|- | |- | ||
| − | ! Logging Method | + | ! Logging Method || Radial Distance for 90% Effect, in || Radial Distance for 90% Effect, cm || Formation Volume Investigated, ft<sup>3</sup> || Formation Volume Investigated, m<sup>3</sup> |
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | Conventional 5.25-in. (13-cm) core | + | | Conventional 5.25-in. (13-cm) core || 2.6 || 6.6 || 1.5 || 0.04 |
| − | | 2.6 | ||
| − | | 6.6 | ||
| − | | 1.5 | ||
| − | | 0.04 | ||
|- | |- | ||
| − | | Gamma-gamma log | + | | Gamma-gamma log || 8 || 20 || 17 || 0.5 |
| − | | 8 | ||
| − | | 20 | ||
| − | | 17 | ||
| − | | 0.5 | ||
|- | |- | ||
| − | | Neutron log | + | | Neutron log || 14 || 36 || 40 || 1.1 |
| − | | 14 | ||
| − | | 36 | ||
| − | | 40 | ||
| − | | 1.1 | ||
|- | |- | ||
| − | | Sonic log | + | | Sonic log || 18 || 46 || 59 || 1.7 |
| − | | 18 | ||
| − | | 46 | ||
| − | | 59 | ||
| − | | 1.7 | ||
|- | |- | ||
| − | | Borehole gravity log | + | | Borehole gravity log || 600 || 1,500 || 78,532 || 2,224 |
| − | | 600 | ||
| − | | 1,500 | ||
| − | | 78,532 | ||
| − | | 2,224 | ||
|} | |} | ||
==Logging procedure== | ==Logging procedure== | ||
| − | In a typical logging operation, several downhole station locations are planned ahead of time. The tool is fitted to a conventional wireline and lowered to each station. Once the tool is stopped (in some wells it must be clamped to the side of the well), the measurement begins. The gravity values are telemetered to an operator at the surface. Because of vibrations, seismic activity, or residual tool movement, the measurements may take some time to settle to an acceptable noise level. | + | In a typical logging operation, several downhole station locations are planned ahead of time. The tool is fitted to a conventional wireline and lowered to each station. Once the tool is stopped (in some wells it must be clamped to the side of the well), the measurement begins. The [[gravity]] values are telemetered to an operator at the surface. Because of vibrations, seismic activity, or residual tool movement, the measurements may take some time to settle to an acceptable noise level. |
==Tool limitations== | ==Tool limitations== | ||
| Line 83: | Line 60: | ||
* [[Borehole gravity: uses, advantages, and disadvantages]] | * [[Borehole gravity: uses, advantages, and disadvantages]] | ||
* [[Borehole gravity applications: examples]] | * [[Borehole gravity applications: examples]] | ||
| + | * [[Borehole gravity]] | ||
==References== | ==References== | ||
| Line 94: | Line 72: | ||
[[Category:Predicting the occurrence of oil and gas traps]] | [[Category:Predicting the occurrence of oil and gas traps]] | ||
[[Category:Applying gravity in petroleum exploration]] | [[Category:Applying gravity in petroleum exploration]] | ||
| + | [[Category:Treatise Handbook 3]] | ||
Latest revision as of 18:07, 24 January 2022
| Exploring for Oil and Gas Traps | |
| |
| Series | Treatise in Petroleum Geology |
|---|---|
| Part | Predicting the occurrence of oil and gas traps |
| Chapter | Applying gravity in petroleum exploration |
| Author | David A. Chapin, Mark E. Ander |
| Link | Web page |
| Store | AAPG Store |
How the tool measures gravity[edit]
Figure 1 Fundamentals of measuring density using a borehole gravity sensor. From Schowalter;[1] courtesy AAPG.
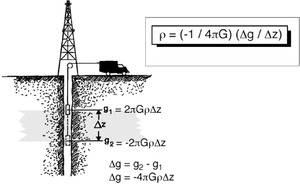
Figure 1 illustrates the fundamentals of measuring density using a borehole gravity sensor. Two gravity measurements, g1 and g2, are made downhole, separated in depth by Δz. The value G is the universal gravity constant. Thus, the gravity gradient, Δg/Δz, is related directly to the density of the intervening layer. The result is a direct computation of the bulk density of that layer.
Depth of investigation[edit]
Figure 2 Depth of investigation is tunable by means of varying the separation between two gravity measurements, Δz. After McCulloh et al.[2] Copyright: SPWLA.
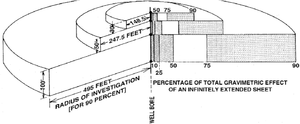
Figure 2 shows how the depth of investigation is tunable by means of varying the separation between two gravity measurements, Δz. The rule of thumb is that 90% of the gravity effect can be imaged at a distance away from the borehole within five times Δz.
Depth of investigation of various logging methods[edit]
The following table, based on data from Beyer[3] shows conservative estimates of the depth of investigation using various density logging tools. Borehole gravity can sample the farthest distance and investigate the most formation.
| Logging Method | Radial Distance for 90% Effect, in | Radial Distance for 90% Effect, cm | Formation Volume Investigated, ft3 | Formation Volume Investigated, m3 |
|---|---|---|---|---|
| Conventional 5.25-in. (13-cm) core | 2.6 | 6.6 | 1.5 | 0.04 |
| Gamma-gamma log | 8 | 20 | 17 | 0.5 |
| Neutron log | 14 | 36 | 40 | 1.1 |
| Sonic log | 18 | 46 | 59 | 1.7 |
| Borehole gravity log | 600 | 1,500 | 78,532 | 2,224 |
Logging procedure[edit]
In a typical logging operation, several downhole station locations are planned ahead of time. The tool is fitted to a conventional wireline and lowered to each station. Once the tool is stopped (in some wells it must be clamped to the side of the well), the measurement begins. The gravity values are telemetered to an operator at the surface. Because of vibrations, seismic activity, or residual tool movement, the measurements may take some time to settle to an acceptable noise level.
Tool limitations[edit]
There are three major problems with the present tool.
- It is large. The smallest typical configuration is 4⅛″ OD, but more widely used configurations are up to 5¼″.
- Because the sensor must be set to vertical to make a reading, it can only measure in wells of 14° deviation or less.
- It takes a long time to make measurements, and it is not a continuous logging tool. The wireline must stop at each individual station, and the tool takes an average of 5–15 min per station for a reading. This means a typical borehole gravity logging operation can run from 24 to 48 hrs.
For the most part, these problems are engineering limitations of the present tool that could be overcome with new and modern sensor development. There is an active project underway to redesign the present tool to make it more useful in modern wells.
See also[edit]
- Borehole gravity methods
- Borehole gravity: uses, advantages, and disadvantages
- Borehole gravity applications: examples
- Borehole gravity
References[edit]
- ↑ Schowalter, T. T., 1979, Mechanics of secondary hydrocarbon migration and entrapment: AAPG Bulletin, vol. 63, no. 5, p. 723–760.
- ↑ McCulloh, T. H., J. R. Kandle, J. E. Schoellhamer, 1968, Application of gravity measurements in wells to problems of reservoir evaluation: Transactions of the 9th Annual SPWLA Logging Symposium. Fundamental work describing the distance of sources seen by the borehole gravity meter.
- ↑ Beyer, L. A., 1991, Borehole gravity Surveys: SEG Short Course notes, June, 350 p.
External links[edit]
| find literature about Borehole gravity tool |
|
|
|
|