Water saturation distribution in a reservoir
| Exploring for Oil and Gas Traps | |

| |
| Series | Treatise in Petroleum Geology |
|---|---|
| Part | Predicting the occurrence of oil and gas traps |
| Chapter | Predicting reservoir system quality and performance |
| Author | Dan J. Hartmann, Edward A. Beaumont |
| Link | Web page |
| Store | AAPG Store |
The distribution of water saturation (Sw) values within a reservoir depends on the height above free water, hydrocarbon type, pore throat-size distribution, and pore geometry. Mapping Sw distribution in a reservoir helps us predict trap boundaries.
BVW[edit]
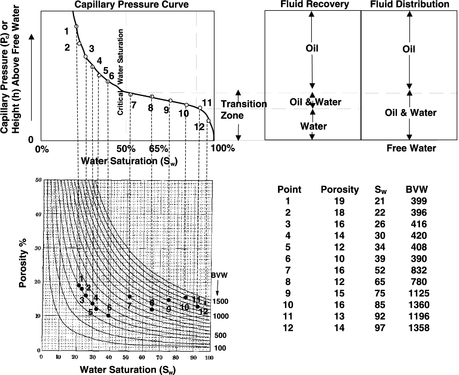
Figure 1 How a Buckles plot relates to capillary pressure, fluid distribution, and fluid recovery in a reservoir.
Bulk volume water (BVW) equals porosity (Φ) × Sw. In zones with the same pore type and geometry, BVW is a function of the height above the free water level. Above the transition zone, BVW is fairly constant. Below the transition zone, BVW is variable.
A Buckles plot is a plot of Sw vs. porosity. Contours of equal BVW are drawn on the plot.
- Points plot on a hyperbolic BVW line where the formation is near immobile water if the points come from a reservoir with consistent pore type and pore geometry.
- Points scatter on a Buckles plot where the formation falls below the top of the transition zone.
Figure 1 shows how a Buckles plot relates to capillary pressure, fluid distribution, and fluid recovery in a reservoir.
Limitations of BVW[edit]
BVW and Buckles plots can be confusing in interbedded lithologies or in areas where facies changes occur because of changing pore types.
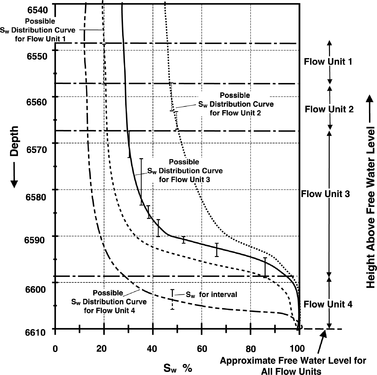
Sw–depth plots[edit]
These illustrate how Sw varies within a hydrocarbon-bearing zone. Variations reflect different pore types and/or height above free water. An Sw–depth plot can be used to delineate three things:
- Transition and waste zones
- Flow units
- Containers
Individual plots can be prepared for wells along dip and strike and correlated to show Sw changes across a reservoir or field. Figure 2 is a hypothetical example of an Sw–depth plot with estimated Sw distribution curves for several flow units for a hydrocarbon-bearing zone in a well.
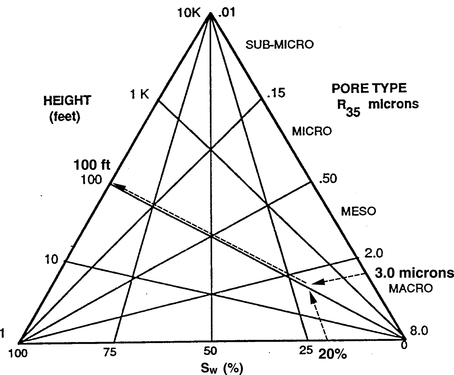
Height–sw–pore type diagram[edit]
The empirical ternary diagram in Figure 3 is handy for estimating either height above free water, pore type (r35), or Sw for a flow unit when the other two variables are known. For example, if Sw for a flow unit is 20% and the pore type is macro with a port size of approximately 3μ, then the height above free water for the flow unit is approximately length::100 ft. Assumptions for the diagram include 30°API gravity oil, saline formation water, and a water-wet reservoir.