Rock quality

Exploring for Oil and Gas Traps
Series	Treatise in Petroleum Geology
Part	Predicting the occurrence of oil and gas traps
Chapter	Predicting reservoir system quality and performance
Author	Dan J. Hartmann, Edward A. Beaumont
Link	Web page
Store	AAPG Store

Methods

Analyzing air permeability (K_a and porosity (Φ) data separately to characterize rock quality can be deceiving. Analyzing K_a and Φ data using the K_a/Φ ratio or the r₃₅ method is much more effective for determining quality. The K_a/Φ ratio or the r₃₅ method yields information about the fluid flow and storage quality of a rock.

Which is better rock?

Figure 1 SEM microphotographs.

Using K_a and Φ data separately to characterize reservoir rock quality is misleading. Consider the rocks shown in the SEM microphotographs in Figure 1. Flow unit 1 is a mesoporous, sucrosic dolomite. Its average Φ is 30% and average K_a is 10 md. Flow unit 2 is a macroporous, oolitic limestone. Its average Φ is 10% and average K_a is 10 md.

Initially, we might think that flow unit 1 is higher quality because it has three times more porosity and the same permeability as flow unit 2. However, in terms of fluid flow efficiency and storage, as shown by the K_a/Φ ratio or r₃₅, flow unit 2 is actually the better rock.

In a reservoir section, increasing Φ and constant K_a indicate pores are becoming more numerous and smaller and pore surface area is increasing. Immobile water saturation for a reservoir (S_w) becomes greater as more surface is available to the wetting fluid. Higher immobile S_w decreases the available pore storage space for hydrocarbons. Also, as the pore size decreases, so does the pore throat size. Flow unit 2 above is the better reservoir rock because it has larger pore throats and lower immobile S_w. K_a/Φ ratio or r₃₅ accounts for the interrelationship of K_a and Φ, making them effective methods for comparing rock quality.

What is the k_a/Φ ratio?

K_a and Φ are standard components of many reservoir engineering wellbore flow performance equations. The K_a/Φ ratio reflects rock quality in terms of flow efficiency of a reservoir sample. When clastics and carbonates are deposited, they have a close correlation of particle size to the K_a/Φ ratio. Mean pore throat radius increases as grain or crystal size increases, but modification to grain shape and size tends to “smear” the distribution.

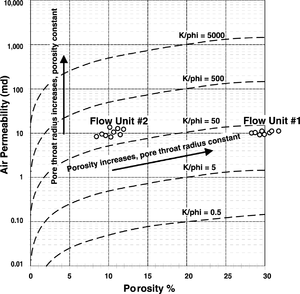
In Figure 1, flow unit 1 has a K_a/Φ value of 33 and flow unit 2 has a K_a/Φ value of 100. Even though Φ is greater and K_a is the same for flow unit 1, the lower K_a/Φ value indicates its quality is lower than flow unit 2.

K_a/Φ plot

Figure 2 Contour plot.

On the plot in Figure 2, the contours represent a constant K_a/Φ ratio and divide the plot into areas of similar pore types. Data points that plot along a constant ratio have similar flow quality across a large range of porosity and/or permeability. The clusters of points on the plot in Figure 2 represent hypothetical K_a/Φ values for flow units 1 and 2 presented in Figure 1. The position of the clusters relative to the K_a/Φ contours indicates flow unit 2 has higher quality in terms of K_a/Φ ratio than flow unit 1.

What is r₃₅?

Figure 3 Capillary pressure curve and pore throat size histogram. Modified from Doveton.

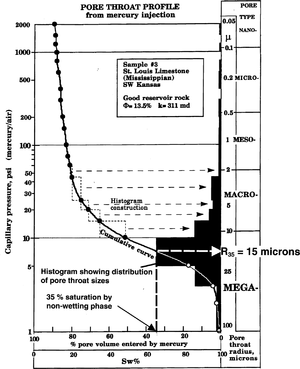
H.D. Winland of Amoco used mercury injection-capillary pressure curves to develop an empirical relationship among Φ, K_a, and pore throat radius (r). He tested 312 different water-wet samples. The data set included 82 samples (56 sandstone and 26 carbonate) with low permeability corrected for gas slippage and 240 other uncorrected samples. Winland found that the effective pore system that dominates flow through a rock corresponds to a mercury saturation of 35%. That pore system has pore throat radii (called port size, or r₃₅) equal to or smaller than the pore throats entered when a rock is saturated 35% with a nonwetting phase. After 35% of the pore system fills with a non-wetting phase fluid, the remaining pore system does not contribute to flow. Instead, it contributes to storage.

Pittman speculates, “Perhaps Winland found the best correlation to be r₃₅ because that is where the average modal pore aperture occurs and where the pore network is developed to the point of serving as an effective pore system that dominates flow.” The capillary pressure curve and pore throat size histogram in Figure 3 illustrate Pittman's point.

The winland r₃₅ equation

Winland developed the following equation to calculate r₃₅ for samples with intergranular or intercrystalline porosity:

$\log {\mbox{r}}_{35}=0.732+0.588\log {\mbox{K}}_{\rm {a}}-0.864\log \Phi$

where:

• K_a = air permeability, md
• Φ = porosity, % (not decimals)

Solving for r:

${\mbox{r}}_{35}=10^{0.732+0.588\log {\rm {K}}_{\rm {a}}-0.864\log \Phi }$

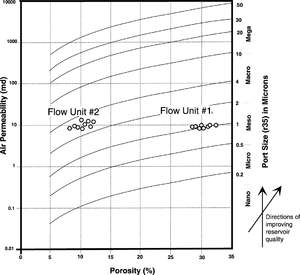
Characterizing rock quality with r₃₅

Figure 4 K_a/Φ plot.

Rock quality is easily characterized using r₃₅. Consider the clusters of points representing flow units 1 and 2 (Figure 1) on the K_a/Φ plot in Figure 4. The diagonal curved lines represent equal r₃₅ values. Points plotting along the same lines represent rocks with similar r₃₅ values and have similar quality. By interpolation, r₃₅ for flow unit 1 is approximately 1.1μ, and r₃₅ for flow unit 2 is approximately 3μ. The r₃₅ in flow unit 2 is almost three times as large as flow unit 1. Therefore, flow unit 2 has better flow quality.

Advantages of r₃₅ over k_a/Φ ratio

Using r₃₅ instead of the K_a/Φ ratio for characterizing rock quality of water-wet rocks has advantages:

• r₃₅ is an understandable number; K_a/Φ ratio is a dimensionless number
• r₃₅ can be determined from capillary pressure analysis and related to K_a/Φ values
• If two variables are known (K_a, Φ, or r₃₅), then the other variable can be calculated using Winland's equation or estimated from a K_a/Φ plot with r₃₅ contours

Example capillary pressure curves

• 

  Figure 5 Hypothetical capillary pressure curves.

• 

  Figure 6 Hypothetical drainage relative permeability curves.

Hypothetical capillary pressure curves can be drawn by using r₃₅ as a point on the curve. The capillary pressure curves below are hypothetical curves for the example presented in Figure 4. The curves demonstrate that entry pressures for flow unit 2 are less than those for flow unit 1; therefore, fluid flow in flow unit 2 is more efficient. In Figure 5, it takes length::28 ft of oil column for oil to enter 35% of pore space of flow unit 2 and length::70 ft to enter 35% of pore space of flow unit 1.

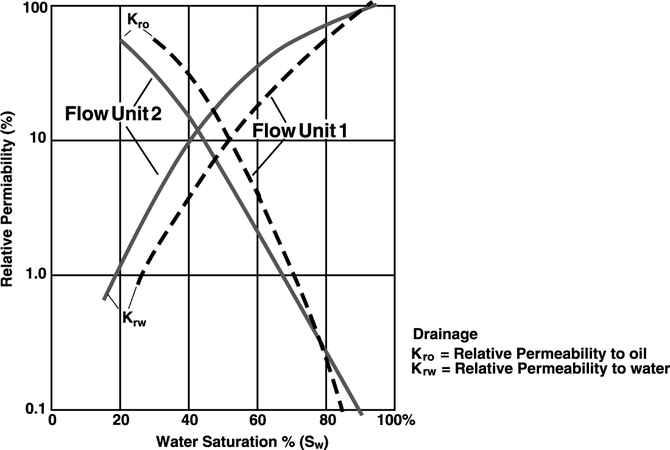
Example relative permeability curves

Figure 6 depicts hypothetical drainage relative permeability curves to represent flow units 1 and 2.

See also

• Pore-fluid interaction
• Hydrocarbon expulsion, migration, and accumulation
• Pc curves and saturation profiles
• Converting Pc curves to buoyancy, height, and pore throat radius
• What is permeability?
• Relative permeability and pore type

External links

find literature about Rock quality

• Original content in Datapages
• Find the book in the AAPG Store