Permeability
| Development Geology Reference Manual | |

| |
| Series | Methods in Exploration |
|---|---|
| Part | Laboratory methods |
| Chapter | Permeability |
| Author | Henry A. Ohen, David G. Kersey |
| Link | Web page |
| Store | AAPG Store |
Permeability is the capacity of a rock layer to transmit water or other fluids, such as oil. The standard unit for permeability is the Darcy (d) or, more commonly, the millidarcy (md). Relative permeability is a dimensionless ratio that reflects the capability of oil, water, or gas to move through a formation compared with that of a single-phase fluid, commonly water. If a single fluid moves through rock, its relative permeability is 1.0. Two or more fluids generally inhigit flow through rock compared with that of a single phase of each component.[1]
Theoretical background
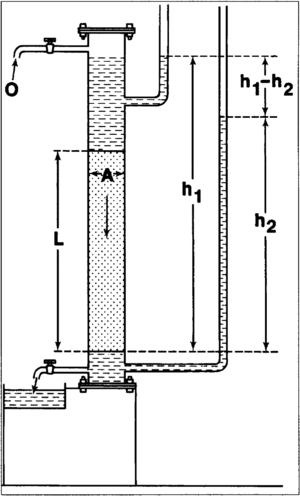
The fundamental relationship given by Henry[3] is the basis for permeability determination. Darcy's law originates from the interpretation of the results of the flow of water through an experimental apparatus, shown in Figure 1. In this experiment, water was allowed to flow downward through the sand pack contained in an iron cylinder. Manometers located at the input and output ends measured fluid pressures, which were then related to flow rates to obtain the following fundamental Darcy's law:
where
- q = water flow rate
- K = constant of proportionality that is characteristic of the sand pack
- A = cross-sectional area of the sand pack
- Δh = h1–h2 = difference in height between the water levels in the manometers
- L = length (cm)
The units in which permeability is typically expressed are the darcy (d) and millidarcy (md). A permeability of 1 d allows the flow of 1 cm3 per second of fluid with 1 cP (centipoise) viscosity through a cross-sectional area of 1 cm2 when a pressure gradient of 1 atm/cm is applied. This definition unfortunately contains nonconsistent units, as pressure is expressed in atmospheres rather than in fundamental units. Lowman et al.,[4] however, have redefined the darcy unit in the mks system in which square meters represents the standard dimension of permeability. The millidarcy, which is one-thousandth of a darcy, is commonly used in core analysis and oilfield operations.
Factors controlling permeability
Pore geometry
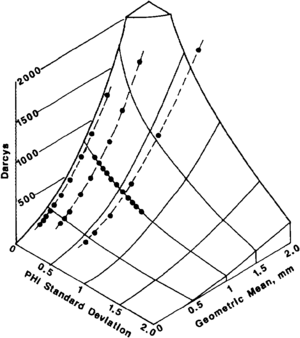
Permeability is a function of the geometry of the pore structure of the porous media. Permeability is controlled in sandstone by grain size, grain orientation, packing arrangement, cementation, clay content, bedding, and grain size distribution and sorting. In carbonates, permeability is a function of the degree of mineral alteration (such as dolomitization), porosity development, and fractures. Figure 2 shows the relationship among permeability, sorting, and grain size.
Bedding
Directional and local variations of permeability generally exist in reservoirs. Permeability perpendicular to bedding planes (vertical permeability) is typically lower than horizontal permeability (parallel to the bedding planes).
Porosity
Several attempts have been made in the past to derive a general relationship between porosity and permeability. Prominent among these relationships is the work of Kozeny,[7] which considered the porous media as a bundle of capillary tubes of equal length. Modifications to account for tortuosity of flow paths in the porous media have been proposed, including the Carman-Kozeny model (1938). Unfortunately, only qualitative results have been obtained using these permeability-porosity relationships because of the complexity of the geometry of the porous media.
Berg[8] suggested that a better understanding of the properties of the rock that control size, shape, and continuity of the rock is the key to relating fluid flow properties to reservoir rock properties. Qualitatively, it is reasonable to assume that permeability should increase with increase in porosity in unfractured reservoirs without significant diagenetic alterations. In fact, it has been shown that there is a relationship between porosity and permeability within units with the same hydraulic properties.[9] (For more on porosity, see Porosity and Core-log transformations and porosity-permeability relationships.)
Confining pressure
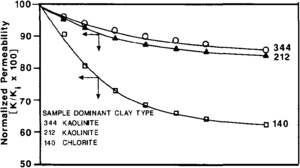
Permeability decreases with increasing confining pressure. Unconsolidated or poorly lithified rock undergoes much greater permeability reduction under confining pressure than well-consolidated rock. As shown in Figure 3, a greater percentage of permeability reduction is typically observed in lower permeability rock than in higher permeability rock. To determine permeability-stress relationships, which are representative of in situ reservoir conditions, permeability measurements should be made on selected samples at a series of confining pressures. Jones[10] has recently presented a method that allows a two-point determination of a permeability-stress model that reduces the required number of permeability measurements under confining stress for permeability-stress prediction.
Permeability determination
Theoretical basis
Permeability is not measured; it is calculated. Therefore, although it is a rock property and a constant for a given core sample, permeability values can vary according to the model and boundary conditions used in the calculation. To determine permeability, Darcy's law inherently assumes constant fluid properties. Modifications of Darcy's law[11] take into account differences in viscosity and density. Thus, permeability can be determined with fluids other than water as long as these fluids are nonreactive. Because permeability is often measured with gases, two additional boundary conditions—gas slippage and inertial effects—must be considered.
Gas slippage and inertial effect
When gas is used to determine permeability at low mean pressure, the resistance to flow from drag is very low, resulting in “gas slip conditions.” Consequently, permeability calculated from Darcy's law will be too high and must be corrected using the Klinkenberg[12] model. When gas permeability is corrected for slippage effects at the fluid/pore wall interface, it is called equivalent, nonreactive, liquid permeability or Klinkenberg permeability.
At high flow rates, gas flowing through porous media accelerates at pore throats and decelerates in pore bodies, giving rise to what is called inertial effects. Non-Darcy flow has been described by Forchheimer,[13] who presented modifications.
Laboratory methods for permeability determination
Liquid and gas permeability can be determined on core samples in the laboratory. However, gas permeability is determined most frequently because sample preparation is simplified and the analytical procedure is fairly rapid. Two methods currently exist for gas permeability determination: steady-state and unsteady-state.
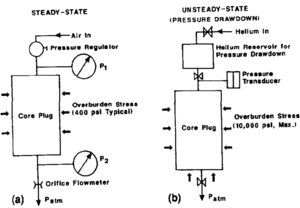
Gas permeability by steady-state method
A simplified schematic diagram of the steady-state apparatus is shown in Figure 4a. The apparatus includes a pressurized gas cylinder, a Hassler core holder, and a flowmeter. The apparatus is designed to ensure that no restrictions exist in flow lines that could cause a pressure drop between the core face and the pressure gauges. To determine air permeability, a clean, dried core sample is first placed in the core holder and pressure is applied to the rubber sleeve to seal it to the core. Air is then injected at a constant pressure until gas production rate and pressure stabilize. The pressure differential between the two ends of the core and flow rate are recorded for permeability calculation using the integrated form of Darcy's law for a compressible fluid. Thus,
where
- ka = air permeability, md
- pa = atmospheric pressure, atm
- p1 = upstream pressure, atm
- p2 = outlet pressure, atm
- L = length, cm
- μ = air viscosity, cP
- qa = gas flow rate at atmospheric pressure, cm3/sec
- A = cross-sectional area, cm2
and where
Measurements are usually made at several gas flow rates to ensure that flow conditions satisfy Darcy's law. In practice, gas permeability is calculated from the slope of the plot of Va versus (p12 - p22)/L, which results in a straight line passing through the origin as long as the conditions for Darcy's flow are maintained. The steady-state method has been the industry standard for many years because it is a convenient technique and the equipment is easy to operate.
Gas permeability by unsteady-state method
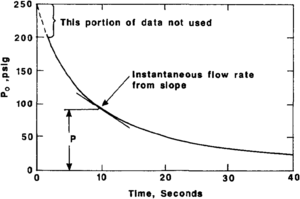
Aronofsky[15] has discussed the theory of transient permeability measurements, and the development of transient state permeameters has been discussed by Wallick and Aronofsky,[16], Champlin (1962)[citation needed], Morris,[17] and Jones.[14]
A schematic diagram of the unsteady-state Klinkenberg permeameter (Jones, 1990)[citation needed] is shown in Figure 4b. The permeameter works on the principle of transient analysis of pressure pulse decay in which Klinkenberg permeability is determined as a function of gas (ideally helium) pressure decay. This equipment consists of a reference cell of known volume that charges the core sample with gas. A downstream valve vents the gas pressure, and pressure change as a function of time is recorded. A typical pressure drawdown plot (Jones, 1990)[citation needed] is shown in Figure 5. Advantages of the unsteady-state method include the ability to determine simultaneously (from Figure 5) the Klinkenberg permeability (k∞ helium slippage factor (βHe), and the inertial coefficient (β). A comparison of the steady-state method to the unsteady-state method is presented in Table 1.
| Steady-State | Unsteady-State |
|---|---|
| Industry standard for 30 years | Determines more representative permeability k∞ instead of kair at reservoir conditions |
| Convenient to use | Enhanced accuracy results from measurement of pressure versus time instead of rate |
| Permeability is determined at low confining pressures | Measures additional reservoir description parameters: β and b |
| Develops practical link with historical data |
Liquid permeability by steady-state method
Water or oil permeabilities are determined on core samples after first obtaining the permeabilities to gas on the extracted dry samples. The sample is saturated with the test fluid, it is placed in a Hassler cell, and pressure is applied to the sleeve. Filtered, gas-free liquid is flowed through the sample, and the rates and pressure drops are measured. Permeability to liquid is calculated as follows:
where
- k1 = liquid permeability, md
- L = length, cm
- μ1 = liquid viscosity, cP
- q1 = gas flow rate at atmospheric pressure, cm3/sec
- A = cross-sectional area, cm2
- Δp = pressure drop, atm
As a quality control device, absolute permeability calculated for water or oil should agree with the k^ calculated for gas permeability.
Liquid permeability by unsteady-state method
A technique based on pulse decay analysis[18] has been developed recently to determine effective permeability to liquid for low quality reservoir rocks. The authors reviewed computational techniques and experimental protocols for liquid permeability determination. A technique that allows the simultaneous determination of liquid permeability and compressibility was also developed. A detailed discussion of this technique is beyond the scope of this article, therefore, interested readers are referred to Amaefule and Masuo.[18]
Permeability averaging and uncertainty determination
It is necessary to average permeability determined for each pay zone to obtain permeability distribution. The most commonly used method to average horizontal permeability is the arithmetic average. Comparison of core permeabilities shows that arithmetic average permeabilities values generally agree with well test permeabilities.
Systematic and/or random errors may affect the accuracy of permeability determined from any method, whether laboratory core or well test analysis. Uncertainty in the models used for permeability determination and input variables can result only in random errors if the same analytical technique, equipment calibration, and quality control scenario are considered. Amaefule and Keelan[19] have shown that random errors can be addressed through stochastic modeling in which uncertainty can be assigned to the independent variables by multiple measurements and statistical calculations. Typically, accuracy of measured permeabilities decline at low and high values and are usually within ±5%.[20]
Useful link
See also
- Core description
- Porosity
- Relative permeability
- Wettability
- Capillary pressure
- SEM, XRD, CL, and XF methods
- Overview of routine core analysis
- Core-log transformations and porosity-permeability relationships
References
- ↑ Peters, Kenneth E., David J. Curry, and Marek Kacewicz, 2012, An overview of basin and petroleum system modeling: Definitions and concepts, in Peters, Kenneth E., David J. Curry, and Marek Kacewicz, eds., Basin modeling: New horizons in research and applications: AAPG Hedberg Series no. 4, p. 1-16.
- ↑ Folk, R. L., 1959, Practical petrographic classification of limestones: AAPG Bulletin, v. 43, p. 1–38.
- ↑ Darcy, H., 1856, Les Fontaines Publiques de la Ville de Dijon: Paris, Victor Dalmont, p. 590–594.
- ↑ Lowman, S. W., 1972, Definition of selected groundwater terms—revisions and conceptual refinements: U. S. Geological Survey Water Supply Paper 1988, 21 p.
- ↑ Pettijohn, F. J., 1975, Sedimentary rocks, 3rd ed.: New York, Harper and Row, p. 628.
- ↑ Krumbein, W. C., and G. D. Monk, 1943, Permeability as a function of the size parameters of unconsolidated sands: American Institute of Mining and Metallurgical Engineers, Technical Publication 1492. 11 p.
- ↑ Kozeny, J. S., 1927, Uber Kapillare Leitung des Wassers im Boden (Aufstieg, Versickerung und Anwendung auf die Bewasserung): S.-Ber. Wiener Akad. Abt. II a, v. 136, p. 271–306.
- ↑ Berg, R. R., 1970, Method for determining permeability from reservoir rock properties: Transactions Gulf Coast Association of Geological Societies, v. 20, p. 303–317.
- ↑ 9.0 9.1 Amaefule, J. O., Keelan, D. K., Kersey, D. G., Marschall, D. M., 1988, Reservoir description—a practical synergistic engineering and geological approach based on analysis of core data: 63rd SPE Annual Technical Conference and Exhibition of the Society of Petroleum Engineers, Houston, TX, October 2–5, SPE 18167.
- ↑ Jones, S. C., 1988, Two-point determinations of permeability and PV versus net confining stress: Society of Petroleum Engineer Formation Evaluation, v. 3, p. 235–241.
- ↑ Muskat, M., 1937, Flow of Homogeneous Fluids Through Porous Media: New York, McGraw Hill, 287 p.
- ↑ Klinkenberg, L. J., 1941, The permeability of porous media to liquid and gases, in Drilling and Production Practices: Washington, D., C., American Petroleum Institute, p. 200–211.
- ↑ Forchheimer, P. H., 1901, Wasserbewegung durch Boden: Zeitschrift Verein Deutscher Ingenieure, v. 45, n. 50, p. 1781–1788.
- ↑ 14.0 14.1 Jones, S. C., 1972, Rapid accurate unsteady-state klinkenberg permeameter: Society of Petroleum Engineers Journal, v. 12, p. 383–397., 10., 2118/3535-PA
- ↑ Aronofsky, J. S., 1954, Effect of gas slip on unsteady flow of gas through porous media: Journal of Applied Physics, v. 25, n. 1, p. 48–53., 10., 1063/1., 1721519
- ↑ Wallick, G. C., Aronofsk, J. S., 1954, Effects of gas slip on unsteady flow of gas through porous media—experimental verification.: Transactions of the American Institute of Mining and Engineering, v. 201, p. 322–324.
- ↑ Morris, W. L., 1953, Assignor, Philips Petroleum Co. Portable Permeameter: U., S. Patent No. 2,633,015, March 23.
- ↑ 18.0 18.1 Amaefule, J. O., Masuo, S. T., 1986, Use of capillary pressure data for rapid evaluation of formation damage or stimulation: Society of Petroleum Engineers Paper No. 12475.
- ↑ Amaefule, J. O., Keelan, D. K., 1989, Stochastic approach to computation of uncertainty in petrophysical properties: SC Conference Paper No. 8907.
- ↑ Keelan, D. K., 1971, A critical review of core analysis techniques: 22nd Annual Technical Meeting of the Petroleum Society of the Canadian Institute of Mining, Calgary, Banff, Alberta, June 2–5, Paper No. 7612, p. 1–13.
External links
- Original content in Datapages
- Find the book in the AAPG Store
- Dictionary:Permeability in Sheriff's Encyclopedic Dictionary