Risk: expected value and chance of success
Economic analysis of contemplated oil and gas ventures must be carried out on the assumption that the project is successful, with "success" often being expressed as one of several levels of profitability based on the various ranges in geotechnical and economic parameters that impact project commerciality. However, many exploration ventures do not succeed, and not all development wells and projects succeed either, so the consequences of such failure must be considered in appraising the economic merit of a proposed development venture.
Accordingly, the expected value (EV) of any venture can be expressed as follows:
Expected value concept[edit]
Imagine that you have the opportunity to participate in a simple game in which you are asked to correctly call the toss of a fair coin. If your call is correct, you will win $20,000; if it is incorrect, you will win nothing.
| Trial | Outcome | Consequence – Cost | Profit/Loss × Probability = | Risked Result |
|---|---|---|---|---|
| Free trial | Correct call | +cost::20,000 USD – 0 = | +cost::20,000 USD × 0.5 = | +cost::10,000 USD |
| Incorrect call | 0 – 0 = | 0 × 0.5 = | 0 | |
| EV =+cost::10,000 USD | ||||
| cost::10,000 USD trial | Correct call | +cost::20,000 USD–cost::10,000 USD = | +cost::10,000 USD × 0.5 = | +cost::5,000 USD |
| Incorrect call | 0 – cost::10,000 USD = | –cost::10,000 USD × 0.5 = | –cost::5,000 USD | |
| EV= 0 | ||||
| cost::8,000 USD trial | Correct call | +cost::20,000 USD – cost::8,000 USD = | +cost::12,000 USD × 0.5 = | +cost::6,000 USD |
| Incorrect call | 0 – cost::8,000 USD = | –cost::8,000 USD × 0.5 = | –cost::4,000 USD | |
| EV= +cost::2,000 USD | ||||
If you were able to play such a game "for free," the expected value of each trial would be +$10,000. If you had to pay $10,000 each time you played, the EV would be zero, so that, statistically, you then would be "trading dollars." If you were willing to invest $8,000 in one trial of this game, the EV would be +$2,000 (Table 1). In this example, there are only two possible outcomes and you are betting on one trial. It is important to emphasize that in oil and gas exploration, there are many possible outcomes. Furthermore, the concept of expected value as a decision criterion requires repeated trials. The expected value is the average profit per decision assuming repeated trials are made.
Faced with choosing among several options, the decision rule is to select the option having the highest EV. Remember, one alternative is to invest in a risk-free project having some minimum return (net present value = 0 discounted at a risk-free interest rate). Obviously, when operators choose to participate in ventures having negative expected values, they are "betting against the House."
In exploratory ventures, cost of failure usually includes dry hole cost, cost of lease bonuses of the condemned leases, and some G & G costs. For development ventures, some substantial additional capital investments may also occur, plus expense items that will have to be written off as well—expenditures that were needed to determine the viability of the project, such as several completed wells, equipment, materials, and supplies.
Probability of geological success[edit]
Every expression in the expected value equation requires a responsible geotechnical estimate. Uncertainties impacting reserves, revenue, and costs addresses procedures for estimating reserves (the primary component of revenue) and costs (both of success as well as failure). Here we address the problem of assessing the chance of geological success.
For exploratory prospects (including shallow pool, deeper pool, and extension wildcats, commonly managed by development geologists), the recommended procedure is for the geotechnical professional to express his or her confidence independently in four critical geological aspects of any prospect:
- What is the probability (or confidence) that reservoir rock is present, of sufficient porosity and permeability to be productive, and in some minimal thickness and extent sufficient to contain detectable (i.e., measurable) quantities of mobile hydrocarbons, or to tempt a prudent onshore domestic operator to attempt a completion?
- One approach is to estimate the minimum required flow rate and relate this flow rate to thickness and permeability. In any case, what we seek is the geologist's confidence in the existence of at least a minimal reservoir—thickness, extent, porosity, and effective permeability. Under this approach, encountering a wet, commercial-quality sandstone would not be a failure in the reservoir category, but rather in one of the other categories, such as an unexpected structural low, an absence of hydrocarbon charge, or a leaky trap. However, the presence of a 1-ft-thick tight siltstone where a 10-ft-thick porous sandstone objective had been predicted would be a reservoir failure!
- What is the probability (or confidence) that the geological structure of the reservoir objective is, in reality, essentially as represented on maps and cross sections?
- It is important to note here that we do not require an actual "structure," such as a domal anticline or a fault closure, only that prospect maps and sections accurately depict the structural configuration. For example, if only regular monoclinal south dip is required in the case of a stratigraphic trap prospect, then the geologist should express confidence—as a probabilistic estimate—that the structure in the vicinity of the prospect actually is indeed regular monoclinal south dip.
- If the map shows an antithetic fault closure, then what is the probability that such a structural configuration will actually turn out to be present?
- This geological chance factor is formulated to apply to stratigraphic as well as structural traps, and in tacit acknowledgment that the structural map is ordinarily the single most important map involved in most prospects and many development projects. Also, structural "busts" are a common reason for dry holes.[1]
- The geological structure chance factor, in combination with the reservoir requirement, focuses on the geometry of the envisioned oil or gas [[accumulation] and on the volumes of fluids necessary to sustain a production test or prudent drill stem test.
- What is the probability (or confidence) that hydrocarbons are present in the subsurface geological environment such that the prospect has had access to them in some quantity to provide at least some modicum of hydrocarbon charge?
- This geological chance factor deals with such questions as the volumetric adequacy of petroleum source rocks, the generation of oil and/or gas, the migrational pathways to the site of the prospect, and the concentration of hydrocarbons in the reservoir fluid (hydrocarbon saturation of at least 50% is required). The question of timing is not addressed here. In most frontier basins, the hydrocarbon charge issue is very important. In established basins and producing trends, however, its significance tends to be slightly diminished. Obviously, for development projects, the hydrocarbon charge requirement has ordinarily been satisfied.
- What is the probability (or confidence) that a sealed trap exists, based on the lithologic combinations and structural configurations depicted, and that the trapping configuration was already formed when hydrocarbons were migrating into the area of the prospect?
- Here we address three questions. First is the idea of the sealing capability between reservoir and top seals, seat seals, and lateral seals (whether formed by stratigraphic contrasts or sealing faults). Fluid viscosity, bed thickness, differential permeability, and fault history all influence the seal question. The second question is about timing, as noted in item #3 above: if the trapping configuration came into being after migration occurred, then the gate has been shut only after the horse got out. The third question has to do with preservation from subsequent freshwater flushing or degradation of reservoired hydrocarbons. As used here, the term trap has no implications of geometry or configuration—only of containment and sealing. The troublesome issue of "fill-up" (best represented as a percentage) falls into this category. For most development wells, the sealed trap requirement has been satisfied.
The voice of experience warns you that for exploration projects, do not use probabilities of 1.0—you simply cannot be that sure! "Absolute certainty" is 0.9 or 0.95.
The next step is to multiply the decimal fractions representing the four geological chance factors, which produces the probability of geological success, or Psg.
Probability of completion[edit]
The key question for most development geologists is, "What is the probability that this well will be completed?" Thus, the probability of success, or Ps, is really the probability of completion. The probability of geological success (as defined and derived above) can be made to approximate the probability of completion (or the probability of success) by two linked measures:
- Minimum but finite dimensions are required for all reserves parameters, such as area, net pay, and hydrocarbon recovery factor. The concept here is that a small but finite volume of oil or natural gas, and some minimum reservoir thickness and quality, must be present for an accumulation even to be detected by an operator. In other words, the lower limit of an accumulation thus defined is substantially larger than 1 bbl of oil!
- The four geological chance factors are defined so as to include the concept of the practical lower limit, that is, a modicum of porosity, permeability, and thickness of reservoir rock; a closure sufficient to contain an accumulation large enough to sustain a production test (or even a prudent drill stem test); and a hydrocarbon charge and sealing capability sufficient for at least 50% hydrogen saturation.
The probability of success and—by subtracting it from 1.0—its derived counterpart, the probability of failure, or Pf, are the expressions required to calculate the expected value of an exploratory drilling venture. A further modification is necessary for development wells and projects.
| Well Class | U.S. | Canada |
|---|---|---|
| New pool wildcats | 0.53 | 0.48 |
| Deeper pool wildcats | 0.15 | 0.54 |
| Shallower pool wildcats | 0.62 | None reported |
| Outpost (extension) wildcats | 0.42 | 0.68 |
| New field wildcats | 0.14 | 0.30 |
| All exploratory wells | 0.30 | 0.56 |
| All development wells | 0.79 | 0.85 |
When compared with exploration drilling statistics, such as those reported annually by the AAPG Committee on Statistics of Drilling (CSD), Ps was approximately equivalent to their definition of success, that is, that the subject well was completed and did produce some hydrocarbons. This does not mean that the venture was profitable. In fact, this definition of success contains at least four possible outcomes:
- The well was completed as the discovery well for a profitable exploratory project (a commercial success).
- The well was completed because anticipated future production would return a profit on the cost of completing and operating, but not on the full exploratory costs, which are thus viewed as sunk and not recoverable (an incremental success). Ordinarily, no more wells would be drilled on the property by the operator, assuming that the well did not provide other new encouragement.
- The well was completed as an incremental success, but subsequent performance was inadequate to sustain even operating costs, resulting in abandonment a short time later.
- The well was completed for "business reasons," that is, to hold a lease position or to satisfy a contractual or regulatory obligation.
Contemporaneous drilling statistics serve to put all this into proper perspective, as shown in Table 2, which reports 1988 results by different classes of wells.
Probability of commercial success[edit]
For exploration ventures, the recommended method to assess the chance of commercial success is to first identify the minimum field size associated with your firm's definition of the threshold of commerciality, and then to determine what proportion of such fields occur in the natural population of counterpart accumulations in the subject trend, play, or basin. This requires the geologist or engineer to construct a field size distribution, as previously discussed.
Example[edit]
For a given extension project having a predicted mean reserve size of 1,500,000 BOE, the geologist has concluded that the probability of reservoir rock is 0.9, the structural probability is 0.8, and the probability of hydrocarbon charge is 0.9. The chief geological risk concerns whether a key fault will or will not seal, and the geologist assesses this as a 50/50 proposition. Thus, the perceived chance of geological success is 32%. However, construction of a field-size distribution for 20 analogous fault-separated fields in the trend reveals that only 3/4 of them are larger than 200,000 bbl, which is the minimum economic field size in this trend for your firm. Therefore, the chance of commercial success is 0.75 × 0.32 = 0.24. Calculated in this way, 0.24 represents the chance of finding a field of 200,000 bbl or larger.
Applications to development projects[edit]
In development projects, just as in exploration projects, the geological chance factors must be derived from the study of maps, cross sections, and well data. They cannot be "pulled out of the air." However, there is an important difference: the fact that development is contemplated at all implies that a petroleum accumulation exists, so the hydrocarbon charge and seal/trap requirements have generally been satisfied. The only remaining geological risks have to do with (1) structural variations that may depress the reservoir below the oil-water contact and (2) stratigraphic variations affecting both thickness and quality of the reservoir section.
Although individual development wells have a high probability of success, some development dry holes are drilled. Naturally, the proportion of development dry holes will vary according to the geological characteristics of individual fields and trends. Nevertheless, this failure rate is significant and must be anticipated in
- constructing the cash flow model of the development project;
- determining the expected net present value of each development well; and
- anticipating the chance of failure of the entire development project, particularly if it is a small one involving only a few wells.
Moreover, since development wells should generate sufficient production revenues to pay out in less than about 3 years, most operators will not purposefully continue to drill development wells that are only incrementally commercial. Even so, it is still true that many development wells are completed each year that return only enough to pay for completion and operating costs, not the cost to drill them. Nevertheless, the probability of success as applied to development projects should always be the probability of commercial success, which for most development wells should generally be 60-80%.
For enhanced oil recovery projects, the geologist or engineer is well advised to anticipate ranges in final project or process efficiency when constructing future scenarios. In addition, project commerciality may be severely impacted by future negative (or positive) trends in nongeological factors, such as costs, wellhead prices, transportation problems, and time delays. Thus, these contingencies should also be anticipated and expressed probabilistically. Therefore, the probability of commercial success for a development project should have three components: (1) geotechnical, (2) operational, and (3) economic. A key parameter here is the minimum acceptable economic threshold for project performance.
Accordingly, the chance of project success becomes the probability of achieving the minimum acceptable return (or higher). This is related to the probability of finding at least some minimum reserves capable of producing at some minimum rate. At reserves greater than this minimum, the project will be commercial. Thus, the calculation of expected value for development projects is
where ENPV = expected net present value.
Decision tree analysis[edit]
The expected value concept also has important applicability in the analysis of complex and sequential decisions. Here the basic idea is to "map out" the sequence of events, indicating decision and chance nodes as follows:
Probabilities must be assigned to all possible outcomes emanating from chance nodes, but not to branches from decision nodes. Risked values are assigned to each foreseen decision. Decision trees are constructed from left to right and solved from right to left.
Theoretically, the basic decision rule is to always choose the branch having the highest expected value. In practice, however, capital-constrained companies often select a less desirable option due to capital requirements of a higher EV alternative.
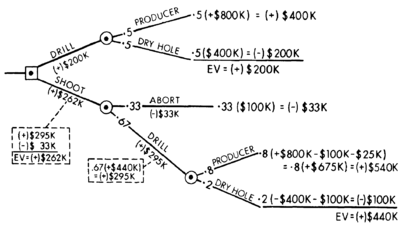
Figure 1 shows a decision tree for a simple development well problem. The problem here is whether to drill a well at the edge of a developing oil field or to shoot a seismic line first to try to determine whether the location may be structurally low and wet and thus move the drill site to the most favorable location. There is also uncertainty about reservoir quality, which cannot be resolved without drilling. The costs in this example are as follows: cost of seismic ($100,000), cost of deferring production to allow time to shoot, process, and interpret seismic ($25,000), cost of dry hole ($400,000), and mean present value of producing well ($800,000, including drilling costs). An analysis of this problem shows two options:
- Option A
- If you drill without shooting seismic, your staff sees two possible outcomes: (1) a 50% chance of a profitable producing well or (2) a 50% chance of a dry hole.
- Option B
- If you first shoot a seismic line, your staff sees the following possible outcomes: (1) a 33% chance of getting a negative seismic result (that is, a structural low) and aborting the project or (2) a 67% chance of getting an encouraging seismic result and therefore drilling the well in the most favorable location. Positive seismic results would be expected to change the odds to an 80% chance of a profitable producer and a 20% chance of a dry hole.
The solution to the problem shown in Figure 1 is option B. It is the preferred choice because it has the higher estimated present value ($262,000 versus $200,000). Thus, the value (or profit) to the project of the additional seismic is +$62,000. Note, however, that if the proposed seismic line costs $200,000, option A becomes the preferred choice ($200,000 versus $161,000), so it would be more cost effective to drill rather than to shoot.
See also[edit]
- Economics: time value of money
- Risk: dealing with risk aversion
- Economics: fundamental equations for oil and gas property evaluation
- Economics: key parameters
- Economics of property acquisitions
- Taxes
- Uncertainties impacting reserves, revenue, and costs
- Cash flow model
References[edit]
- ↑ Rose, P. R., 1987, Dealing with risk and uncertainty in exploration--how can we improve?: AAPG Bulletin, v. 71, n. 1, p. 1-16.
Other resources[edit]
- Newendorp, P. D., 1975, Decision analysis for petroleum exploration: Tulsa, OK, PennWell Books, 668 p.